6

I read this in TCP/IP PROTOCOL SUITE second edition, written by Behrouz A. Forouzan and Sophia Chung Fegan.

In traditional Ethernet, the minimum frame length is 520 bits, the transmission rate is 10 Mbps, the propagation speed is almost the speed of light, and the collision domain is almost 2500 meters.

So what is transmission rate and propagation speed? Why they are not the same?

Robert Harvey
  • 198,589
  • 55
  • 464
  • 673
Tracy
  • 163
  • 1
  • 1
  • 5
  • 3
    Should be on SuperUser or Serverfault – TheLQ Apr 03 '11 at 17:12
  • The book is not quite right about propagation speed. Its a common fallacy that signals propagate down a wire at "about the speed of light". Actually, on most coax and twisted pair wiring the propagation speed is about 2/3 the speed of light - which is actually a LOT less. (Typical figures vary, good cable makers quote it, but something in the region 60% to 70% is pretty normal.) – quickly_now Apr 04 '11 at 09:23
  • 3
    I'm voting to close this question as off-topic because it is not a conceptual programming problem as defined in the **[help center](http://programmers.stackexchange.com/help/on-topic)**. –  May 05 '15 at 02:21

4 Answers4

21

imagine you have a drum. If you beat it 10 times a second that would give you the transmission rate. You can hear it from a hundred meters away in about a second (speed of sound) which is the propogation speed.

Edit: 10 times a second being 10 bits of information send. You can beat faster, increasing the transmission rate, but you can't increase the speed of sound (propogation speed).

Ian
  • 5,462
  • 22
  • 26
3

Propagation speed is the amount of time it takes for one particular signal to get from one point to another.

Transmission Rate is the total amount of data that can be sent from one place to another in a given period of time.

Consider two possibilities at (or close to) opposite extremes:

  1. A 300 baud modem. Propagation speed is close to the speed of light, but transmission rate is only 300 bits per second (~30 characters per second). If, for example, you're talking to a machine 3000 miles away, transmitting a single character is close to instant, but transmitting a lot of them takes a long time (e.g., one megabyte would take close to 10 hours). Propagation speed = ~C, Transmission rate = ~100 KB/hour.

  2. A van/small truck full of hard drives. Let's assume our vehicle can hold 1000 hard drives. Its propagation speed is (roughly) the speed limit from a source to a destination -- let's assume 60 MPH average. To figure the transmission rate, let's assume each hard drive holds 2 terabytes, for a total of 2000 Terabytes. Propagation speed = ~60 MPH, transmission rate = ~40 terabytes/hour.

Jerry Coffin
  • 44,385
  • 5
  • 89
  • 162
  • 2
    Actually, baud rate and bit rate are not the same thing. The baud rate of a device tells us its signaling or symbol rate. The bit rate of a device tells us the information exchange rate or the number of bits per symbol. Multiple bits can be sent per baud. The signal modulation scheme employed determines the number of bits per baud. For example, the bit rate equals the baud rate when BFSK (Binary Frequency-Shift Keying) is used to encode data for transmission. However, 64-QAM (Quadrature Amplitude Modulation) encodes six bits per baud. – bit-twiddler Apr 03 '11 at 22:03
  • @bit-twiddler: yes, but I used a 300-baud modem as my example, and they transmit one bit per baud. It's only when you get to (if memory serves) 9600 bps modems that the two start to differ. – Jerry Coffin Apr 03 '11 at 22:04
  • @Jerry: I just wanted clarify the difference for the OP. The difference between baud rate and bit rate is something that tends to trip up people who are new to data communications. – bit-twiddler Apr 03 '11 at 22:09
  • ＠Jerry why the **transmission rate** is ~40 terabytes/sec,i guess that 2000 divided by 60,but what is the reason to calculate like that ? – Tracy Apr 04 '11 at 03:49
  • @Tracy: per hour, not per second. I was trying to figure both in (multiples of) bytes per hour to make comparison reasonably easy. – Jerry Coffin Apr 04 '11 at 04:18
  • Ah, an update on the old saying "Never underestimate the bandwidth of a station wagon full of mag tape." – David Thornley Apr 04 '11 at 13:43
  • @Jerry sorry,still dont know the logic to get 40 terabytes/hour,how do you get that result ? – Tracy Apr 04 '11 at 16:37
  • 2000 terabytes/50 hours = 40 terabytes/hour. – Jerry Coffin Apr 04 '11 at 16:48
  • @Jeffy so you assume the transmission distance is 3000 miles,right ? – Tracy Apr 05 '11 at 02:46
0

Here's an analogy from Computer Networking: A Top-Down Approach (6th ed.), written by James F. Kurose and Keith W. Ross, found on page 38:

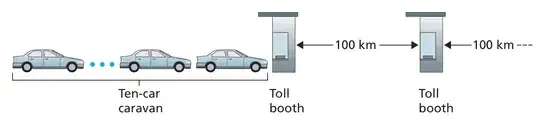
A line of cars approaching a toll booth.

Consider a highway that has a tollbooth every 100 kilometers. You can think of the highway segments between tollbooths as links and the toll- booths as routers. Suppose that cars travel (that is, propagate) on the highway at a rate of 100 km/hour (that is, when a car leaves a tollbooth, it instantaneously acceleratesrates to 100 km/hour and maintains that speed between tollbooths). Suppose next that 10 cars, traveling together as a caravan, follow each other in a fixed order. You can think of each car as a bit and the caravan as a packet. Also suppose that each tollbooth services (that is, transmits) a car at a rate of one car per 12 seconds, and that it is late at night so that the caravan’s cars are the only cars on the highway. Finally, suppose that whenever the first car of the caravan arrives at a tollbooth, it waits at the entrance until the other nine cars have arrived and lined up behind it. (Thus the entire caravan must be stored at the tollbooth before it can begin to be forwarded.) The time required for the tollbooth to push the entire caravan onto the highway is (10 cars)/(5 cars/minute) = 2 minutes. This time is analogous to the transmission delay in a router. The time required for a car to travel from the exit of one tollbooth to the next tollbooth is 100 km/(100 km/hour) = 1 hour. This time is analogous to propagation delay. Therefore, the time from when the caravan is stored in front of a tollbooth until the caravan is stored in front of the next tollbooth is the sum of transmission delay and propagation delay—in this example, 62 minutes.

Austin Moore
  • 113
  • 4
0

The minimum Ethernet frame size is actually 64 octets or 512 bits. The size of the collision domain is bounded by the transmission time of a 512 bit frame. Each bit in a 10Mbps Ethernet frame takes 0.1 microseconds to transmit; therefore, a 512-bit 10Mbps Ethernet frame takes 51.2 microseconds to send. If you dig deeper into the spec, you will find that the size of the collision domain is bounded by the distance that can be traversed, round-trip, in 51.2 microseconds.

bit-twiddler
  • 2,648
  • 1
  • 16
  • 17