Representing mathematical tree structures using software in a compact manner

Question

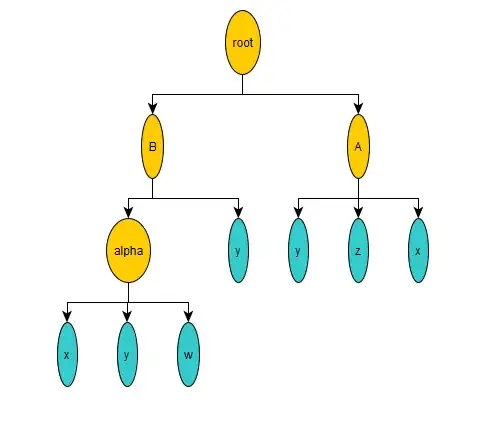
In my work I frequently come across systems of interdependent equations. I have contrived a toy example as follows. The terminal values w, x, y and z are given:

e(y) = A+B

A(y) = x*log(y)+y^z

B(y) = alpha*y

alpha(y) = x*y+w

We could then consider the function e(y) as the root of an arithmetic tree with the following heirarchy:

Previously, in python I would have done something like this to evaluate the result:

import numpy as np

def root(B, A):
    return B+A

def A(x,y,z):
    return x*np.log(y)+y**z

def B(alpha, y):
    return alpha*y

def alpha(x,y,w):
    return x*y+w

if __name__=='__main__':

    x,y,z,w = 1,2,3,4
    result = root(B(alpha(x,y,w),y), A(x,y,z))

This will give me the right result, but I have come to really despise this way of doing things. It requires me to keep track of which arguments each function needs and how the tree itself is built up. Also, suppose I wanted to modify the tree itself by adding branches and leaves. For example, say I wanted to redefine alpha as v+x+y with the new variable v. I'd have to make a new function and a new call, which is not very efficient as I sometimes need to make pervasive and numerous changes.

I tried different approaches to solve this problem as outlined by this question and this question.

I came across a couple of ideas which looked promising, namely function objects and the Interpreter Pattern. However I was disappointed by the Interpreter Pattern. Suppose I didn't create a parser, and went straight for the underlying composite architecture, wouldn't I still have to do something like this?

root = root_obj(B_obj(alpha_obj(x_obj,y_obj,w_obj),y_obj), A(x_obj,y_obj,z_obj))
root.interpret()

The above would require a lot of added complexity for no added value. My question is as follows: What is a simple and useful object oriented paradigm in which I could define, modify and evaluate a mathematical heirarchy in a dynamic manner?

EDIT

Here's an example of what I would like to achieve:

tree = FunctionTree()
tree.add_nodes(root, A, B, alpha, w, x, y, z)
tree.add_edge(root, [A, B])
tree.add_edge(root, A)
tree.add_edge(A, [x,y,z])
tree.add_edge(B, [alpha, y])
tree.add_edge(alpha, [x, y, w])
tree.evaluate()

Yes, this is less "compact" but it is much more flexible. Imaging having methods for deleting and adding new edges. replacing definitions at nodes and reevaluating the result. I am looking for something like this.

Answer 1

This seems to be a continuation of your previous question. The recommendation made in this answer is still valid. But maybe I was not clear enough.

I'm not python fluent, but:

• Create a class AbstractExpression.
• Create a concrete specialisation class for every specific function you have: Function_e, Function_A, Function_B, Function_Alpha. Instances of these class would correspond to your orange boxes.
• Create a concrete class for the terminal expression. Call it Variable, and imagine that every instance of this class has a name. Instance of this class would correspond to your green circles.
• For clarity, let's use the pattern with a function eval(context) instead of interpret(context)

Now to the point on which I was not clear enough:

• Of course, Function_e's constructor would construct a Function_A instance called fA and a Function_B instance. Absolutely no parsing is required here !
• Of course, Function_A would create Variable instances, vy with the names "y", vz for "z" and vx for "x". Again, no parsing is needed: the class constructor construct the needed objects (you code it).
• The Function_e's eval() would do what it needs and call fA.eval() where the result of this functions is needed in the formula. I'll insist: absolutely no parsing takes place here! It's your implementation of e that will call a method of your implementation of A
• in your implementation of fA.eval(), you would call vy.eval(), vz.eval() and vx.eval() in the formula, where you would need each of these variables.

Now we have constructed an interpreter corresponding to your system, (without any parsing), and that is able to calculate the result, if only Variable.eval() could know the values to be used for these parameters. And here enters the context:

• context would be a dictionary that assigns fixed values to variable names.
• context is forwarded as single parameter through all the eval() calls explained above.
• the last implementation needed is eval() for Variable. This would just return the value associated to the variable's name in the context dictionary.

Sorry if I insisted on the absence of parsing. But many web site provide examples of the interpreter pattern without understanding real use cases. So they all are about parsing, which creates significant confusion. You have here a perfect example of use :-)