Toll placement problem (Graph theory)

Question

I'm working on a problem that reduces to something like toll plaza placement on a set of highways. Given a large undirected graph and a list of node pairs with a toll value between them, I need to find the minimal set of toll plaza nodes that can levy the tolls (each plaza node can levy an arbitrary set of tolls). Each node would have a weight that defined how suitable it is to be a toll plaza.

This seems like a common algorithm, but I've never taken graph theory and my searches haven't turned up much. Any pointers on how to solve this would be appreciated!

Graph:

[A]----[1]-----[2]----[3]------[C]
        |              |
        |              |
       [B]            [D]

For example, in this graph, if there are tolls for (A,D) and (B,C), the nodes 1,2,3 would all be equally suitable to levy the tolls, and I could pick one after sorting them by weight. If instead the toll list was:

(A,D) = 5
(B,D) = 6
(B,C) = 7
(A,B) = 1

Then [1] is the only single node that could levy all the tolls. Given lists like these, I want to find the set of "optimal" toll locations like this.

My intuition says this might be a rather difficult problem. I've done some work on a similar problem, where there should be a toll on *every* segment, not just on the paths between specific endpoints. Since the number of nodes was in the thousands and the graph was highly connected, brute force was out of the question and we used various evolutionary algorithms to get a good enough placement. Your problem might be simpler, in particular if the graph is always a tree, as in your example. — amon, Dec 12 '17 at 18:17
Would you be looking for the longest common path between the set of given nodes then? — A_A, Dec 12 '17 at 19:39
@A_A It's not necessarily a common path for the entire set. In the example graph, if I only have tolls for (A,B) and (D,C) then I would want the result to be [1] and [3]. If paths overlap for two tolls, then the result should be on that overlapping portion. — user3298142, Dec 12 '17 at 22:05
So, you would be looking for a) A "Servicing Node" between u,v \in G when the set of corresponding minimum distance paths contains no overlaps, b) The furthest/closest servicing node to u,v \in G when the set of corresponding minimum distance paths does contain overlaps. (?). It will be easier if we formulate what you are after first. — A_A, Dec 13 '17 at 07:10
That's basically it, but I'd want all of the overlapping nodes that minimize the total number of service nodes. If a,b and c,d have no overlapping nodes, then I want a list of nodes between a,b and a separate list of nodes between c,d, since all are equally feasible service nodes. If a,b and c,d have overlapping nodes, then I'm looking for all overlapping nodes. Where I get stuck is in a larger graph. In the second example in my post, there can be a node that minimizes the total number of service nodes across multiple paths. Those are what I'm really after (if they exist). — user3298142, Dec 13 '17 at 17:11
Can there be multiple paths between two end-nodes? Do nodes have an arbitrary number of connections? Are you allowed to have multiple toll booths on a path? Do you have different graphs for each invocation? Or just different node-pairs? Or just different weights? Do you need an exact solution or is an approximation okay? — doubleYou, Dec 16 '17 at 12:01
@doubleYou Yes, in the general case there could be multiple paths between two end-nodes. When that happens, a service node is required on each non-intersecting path (you can't bypass the toll). Nodes may have multiple connections, but in my case never more than 4. The service nodes need to be determined each time a node is added or the policies determining the "tolls" change - that could substantially change the graph and service locations (which is fine). — user3298142, Dec 28 '17 at 21:39
An approximation is fine as long as toll paths always have service nodes along them (that is, there's no way to skip the toll). It doesn't need to be optimal. Obviously more optimal is preferred. — user3298142, Dec 28 '17 at 21:39

doubleYou · Accepted Answer · 2017-12-29T16:47:36.940

Hopefully an expert in graph theory - which I'm not - will swing by at some time to answer this. In the meantime, here are some thoughts that are hopefully of some help.

Naive approach

Obviously, you could try to enumerate all possible paths between all relevant pairs of nodes, and then try to find a valid combination via some commonly used method (graph search over possible configurations/constraint satisfaction/evolutionary algorithms).

However, both the enumeration and the evaluation of a configuration are likely very expensive for non-trivial graphs.

Simple approach

The most simple, and certainly very efficient approach (in terms of runtime) is to just place toll booths next to - or right onto - start/goal nodes. Because you only need to place them before the start or the goal node, you will have at most 4*N booths, where N is the number of node-pairs. The 4 comes from your comment that no node has more than 4 edges.

You can take into account

how many node-pairs a particular node is part of and
how many edges the node has

to reduce the number of total booths. From there, you might be able to optimize further (e.g. using some BFS-variation to check if all paths end up being covered already by other node's toll booths - up to a certain depth).

If this is good enough for you, I'd certainly recommend this approach. But if it was, you probably wouldn't be asking.

(A,B) Separators

Consider only the path from A to B in the graph below. Clearly, a good solution would be the red nodes or the blue nodes.

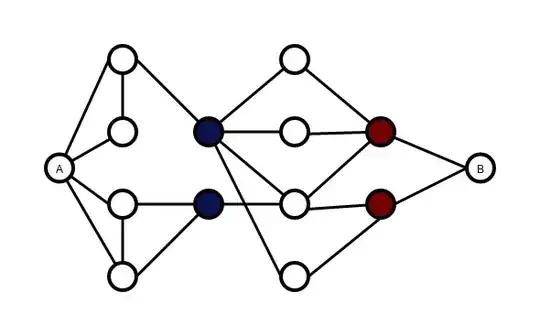
Those are called minimal (a,b) separators and they can be found in polynomial time. A very quick search revealed this, though there may well be better algorithms.

Once you have all minimal (a,b) separators of all pairs, it's time to find a good combination that covers all paths. This should be much easier.

Note that while you should be able to do this in polynomial time, it may still take very long, depending on the size of the graph and the number of pairs.

Other approaches

I have not been able to leverage the fact that you have at most 4 edges per node, but it feels like the kind of thing that would allow for a more efficient approach.

Also, you should look at any further structural information you have about the graph. For example, if you can eliminate dense subgraphs that contain at most one relevant node (that is part of a pair), you might end up with a simpler graph that allows you to make strong assumptions, and hence, use other approaches. Again, I assume you would have mentioned this, but it may be worth another look.

Toll placement problem (Graph theory)

1 Answers1