How to find the shortest path with wormhole nodes?

Question

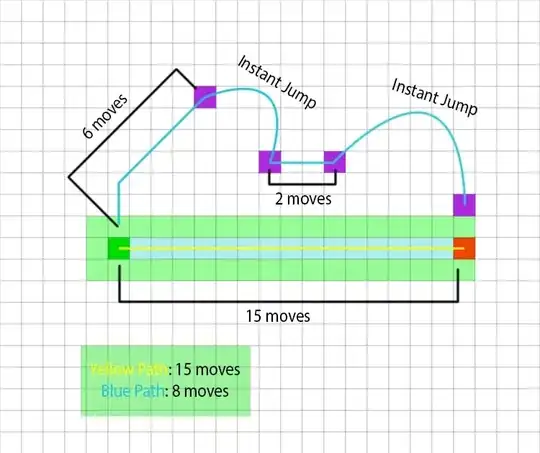
This is an example of what I want to do via code. I know you can use jump point search to easily get from the green node to the red node with no problems, or even A*. But how do you calculate this with warps.

In the image, you can see that it only takes 8 moves to get from the green node to the red node when taking the blue path. The blue path instantly moves your position from one purple node to the next. The space in the middle that costs 2 moves is a point between two warp zones that you must move to get to.

It is clearly faster to take the blue path, since you only need to move half (roughly) as far as the yellow path, but how do I do this programatically?

For the purpose of solving this problem, let's assume that there are multiple purple "warps" around the graph that you are able to use, AND we know exactly where each purple point will warp to, and where they are on the graph.

Some purple warps are bi-directional, and some are not, meaning, sometimes you can only enter a warp from one side, but not go back after warping.

I've thought about the solution, and only concluded that I would be able to calculate the problem by checking the distance to each warp point (minus the uni-directional points), and the difference between those points, and the points close to them.

The program would have to figure out somehow that it is more beneficial to take the second warp, instead of walking from the first jump. So, instead of moving 6 spots, then warping, then moving the remaining 8 steps by foot (which is also faster than not using warps at all), it would take the 6 moves, then the two moves to the second warp.

EDIT: I realized the blue path will actually take 12 moves, instead of 8, but the question remains the same.

Answer 1

Most path finding algorithms are defined in terms of graphs, not in terms of grids. In a graph, a connection between two otherwise distant nodes is not really a problem.

However, you have to take care with your heuristics. With wormholes, the minimum distance between two nodes is no longer the euclidean distance and the distance does not satisfy the triangle inequality. Such heuristics are inadmissible for A*. You therefore cannot use A* easily.

Of course path finding algorithms like Dijkstra that do not use a heuristic will still work. This is more like a breadth-first search and will select your wormholes without extra effort. However, Dijkstra will visit more nodes that A* with a good heuristic. (Dijkstra is equivalent to A* with heuristic(x) = 0.)

I think A* will work if you use a heuristic that treats all outgoing wormholes as a wormhole directly to the target: the heuristic may underestimate the distance, but must never overestimate it. I.e. the heuristic would be:

def wormhole_heuristic(x):
  return min(euclidean_distance(x, g) for g in [goal, wormholes...])

For a very accurate heuristic, you can (recursively) add the distance from the wormhole endpoint to the goal or next wormhole. I.e. as a pre-calculation you could perform path finding on the (totally connected) subgraph containing all wormholes and the goal, where the distance between two nodes is their euclidean distance. This may be beneficial if the number of wormholes is far less than the number of reachable cells on your grid. The new heuristic would be:

def wormhole_heuristic(x):
  direct = euclidean_distance(x, goal)
  via_wormhole = min(euclidean_distance(x, w) + wormhole_path_distance(w, goal) for w in wormholes)
  return min(direct, via_wormhole)

As @Caleth points out in the comments, this is all very tunable and we can improve the first wormhole heuristic without doing a full path finding through the wormhole network, by adding the distance between last wormhole exit and the goal. Because we don't know which wormhole exit will be used last and we must not overestimate, we have to assume the exit closest to the goal:

def wormhole_heuristic(x):
  direct = euclidean_distance(x, goal)
  to_next_wormhole = min(euclidean_distance(x, w) for w in wormholes)
  from_last_wormhole = min(euclidean_distance(w.exit, goal) for w in wormholes)
  via_wormhole = to_next_wormhole + from_last_wormhole
  return min(direct, via_wormhole)

Answer 2

You have a graph with 6 vertices on a grid with co-ordinates:

A ( 0,0)
B ( 4,7)
C ( 7,4)
D (10,4)
E (16,2)
F (16,0)

You can generate a complete graph on those vertices and assign a cost to each edge where the cost is MAX( ABS( x1 - x2 ), ABS( y1 - y2 ) ) for standard edges and a cost of 0 for wormholes.

This will give you the costs (as an adjacency matrix):

   A  B  C  D  E  F
- -- -- -- -- -- --
A  -  7  7 10 16 16
B  7  -  0  6 12 12
C  7  0  -  3  9  9
D 10  6  3  -  0  6
E 16 12  9  0  -  2
F 16 12  9  6  2  -

If there are one-directional warps then only create edges in the graph (or adjacency matrix) that go in that direction but not in the opposite.

You can then use Dijkstra's algorithm with a priority queue.

Start from A and push each adjacent edge onto the priority queue:

Format: (path : cost)

queue     = [ (A-B : 7), (A-C : 7), (A-D : 10), (A-E : 16), (A-F : 16) ]

As the items are pushed onto the queue - keep track of the minimum cost for each vertex and only push paths onto the queue if it is lower cost than the existing minimum cost.

min-costs = { A: 0, B: 7, C: 7, D: 10, E: 16, F: 16 }

Remove the first item from the queue and, if its cost still matches the minimum cost, push all the composite paths formed by that path and its adjacent edges back onto the priority queue (if the composite paths have lower cost than the existing minimum):

Remove: (A-B : 7)

• Try (A-B-A : 14) - reject as higher cost
• Try (A-B-C : 7) - reject as same cost
• Try (A-B-D : 13) - reject as higher cost
• Try (A-B-E : 19) - reject as higher cost
• Try (A-B-F : 19) - reject as higher cost

Remove (A-C : 7)

• Try (A-C-A : 14) - reject as higher cost
• Try (A-C-B : 7) - reject as same cost
• Try (A-C-D : 10) - reject as same cost
• Try (A-C-E : 16) - reject as same cost
• Try (A-C-F : 16) - reject as same cost

Remove (A-D : 10)

• Try (A-D-A : 20) - reject as higher cost
• Try (A-D-B : 16) - reject as higher cost
• Try (A-D-C : 13) - reject as higher cost
• Try (A-D-E : 10) - insert into queue
• Try (A-D-F : 16) - reject as same cost

Now the queue will look like:

queue     = [ (A-D-E : 10), (A-E : 16), (A-F : 16) ]
min-costs = { A: 0, B: 7, C: 7, D: 10, E: 10, F: 16 }

Remove (A-D-E : 10)

• Try (A-D-E-A : 26) - reject as higher cost
• Try (A-D-E-B : 22) - reject as higher cost
• Try (A-D-E-C : 19) - reject as higher cost
• Try (A-D-E-D : 10) - reject as same cost
• Try (A-D-E-F : 12) - insert into queue

Then the queue is:

queue     = [ (A-D-E-F : 12), (A-E : 16), (A-F : 16) ]
min-costs = { A: 0, B: 7, C: 7, D: 10, E: 10, F: 12 }

Remove (A-D-E-F : 12), find that you have got to the destination node in a cost of 12.

Note: the paths (A-B-C-D-E-F), (A-C-D-E-F) and (A-D-E-F) all have the same minimum cost of 12.

Answer 3

Set up a matrix containing all vertices and use the Floyd-Wallenstein-Algorithm or the Bellman-Ford-Algorithm. Both will result in a matrix with the shortest possible paths between all points. You can then iterate through the matrix to find the shortest path connecting two points. (your problem is the same as a asymmetric TSP).