Mapping points to squares

Question

I am working on writing a code for Hilbert algorithm to solve a Traveling Salesmen Problem. Although there are several efficient methods out there, I am just curious about the implementation of Hilbert Space filling curve.

First we create a Hilbert curve and divide the entire area into a number of squares.
Then using the sequence of squares we connect all the points though which the salesmen has to travel.

My problem is on the second part. How can I find the squares which contains a point? Or how can I find the empty squares?

I imagine the details of how to do this may depend on your data structures: how are you representing the points and squares in your program? — FrustratedWithFormsDesigner, Jan 20 '17 at 16:31

ryyker · Accepted Answer · 2017-01-23T14:02:51.057

To find the squares which contains a point, the search domain, i.e. a collection of points, conceptually must contain retrievable attributes, such as number of points, whether a point is to be visited, and even the order in which a point will be visited. An array of a simple struct comes to mind as one implementation that could be used to model such a domain.

in C for example:

typedef struct {
    int x;  //x position in domain
    int y;  //y position in domain
}P; //point

typedef struct {
    P p;
    BOOL occupied; //1 = will be visited, 0 = will NOT be visited
    int sequence;  //0 if not visited, 1-n indicated order of visit.
}DOMAIN;  // example points: {{0, 0}, 1, 1}, {{0, 1}, 0, 0} 
          // meaning:      The point at position 0,0 will be visited first
          //               The point at position 0,1 will not be visited.

//Model of some existing domain using the DOMAIN struct.   
//This one is comprised of 25 points, arranged in 5x5 square,     
//but if a domain of different dimensions is required, (and can   
//be represented in this fashion) modify these initializers to   
//meet those needs:  

DOMAIN domain[] = {{{0,0},1,1},{{0,1},0,-1},{{0,2},0,-1},{{0,3},0,-1},{{0,4},0,-1},
                   {{1,0},0,-1},{{1,1},0,-1},{{1,2},0,-1},{{1,3},0,-1},{{1,4},0,-1},
                   {{2,0},0,-1},{{2,1},1,2},{{2,2},0,-1},{{2,3},0,-1},{{2,4},0,-1},
                   {{3,0},0,-1},{{3,1},0,-1},{{3,2},0,-1},{{3,3},1,3},{{3,4},0,-1},
                   {{4,0},0,-1},{{4,1},1,4},{{4,2},0,-1},{{4,3},0,-1},{{4,4},1,5} };


int main(void)
{   //Get the total number of points existing in domain:
    int pointCount = sizeof(domain)/sizeof(domain[0]);
    int i;

    for(i=0;i<pointCount;i++)
    {   //determine point by point which are to be occupied...
        if(domain[i].occupied == TRUE)
        {   //For any point to be occupied, indicate its location
            //and in what order (sequence) it will be occupied.  
            printf("point[%d,%d] is occupied with sequence %d\n", domain[i].p.x,domain[i].p.y, domain[i].sequence);
        }
    }
    return 0;
}

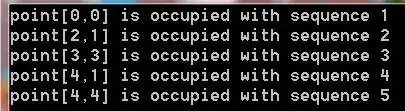
The results of this domain, with points that will be occupied, and the order of occupation:

Thank you so much! I have got any idea after seeing your code and i will try to implement it Python. :) — jhon_wick, Jan 21 '17 at 01:43

Mapping points to squares

1 Answers1