Find nearest best fit for circle

Question

Below is an example image, if I have a point of the white dot in the middle and I want to find the nearest possible location for the blue circle (which is obviously at the location where I placed it) if all the red circles already exist. How can I find that location?

Performance for me is not a major concern for this application.

Answer 1

This is not a general solution, since there are several situations were it will not provide the position of the blue circle with shortest distance to the white dot. For example, if you have 100 red balls grouped together and the white dot is far away from this group of red balls then none of the red balls will have any influence in the position of the blue circle that can just be centered on the white dot. Neither will it show all the calculations details. Anyway, for a subset of configurations, where the solution (blue circle) is tangent to two red circles the following should work:
1) let R be the radius of the blue circle
2) make a loop over all pair of red circles, yes I know this is O(n2).
3) for each pair of circles i,j with centers at (xi,yi) and (xj,yj) with respective radius ri and rj, compute the square of the distance between the pair of circles

d_ij^2=(xi-xj)^2+(yi-yj)^2  

4) put all pairs of circles that

dij^2<R^2

into a list.

5) traverse the list, finding the 2 solutions of circles of radius R tangent to both circles i and j. To do this use these equations together with this image

a = R+ri  
b = R+rj  
c = dij  
α = arccos((b^2+c^2-a^2)/(2bc)  

with above information you can find (X1ij,Y1ij) and (X2ij,Y2ij) the centers of the the 2 circles tangent to circles i and j. For each candidate blue circle loop over all other red circles and see if it don't overlap. If they do discart it if not check distance to white circle. If you keep the one with smaller distance I think you will have the solution when you finish traversing the list of pairs of circles. The algorithm seems like O(n3).

Answer 2

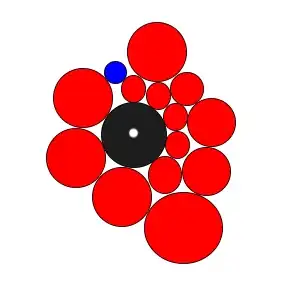
The closest placement to the point will either be on the point, or touching a circle.

therefore, first check the point, then roll the new circle around the edge of each existing circle, calculating the distance from the point and if you overlap as you go and keeping track of the minimum distance point. Stop when you have traversed every circle.

ie. check all points on the green lines, plus the white circle. where the green line is a circle with radius of the red plus the blue

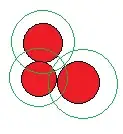
you need to check the whole of the green line, not just intersections so that you cover these edge cases.

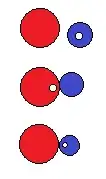
Obviously the step size of your traversal is going to be important in terms of performance. But as you state performance is not an issue, choose the value corresponding to the resolution of your output value. ie float, long?

clarification:

my suggestion is to brute force all points around each circle testing for overlap with all other circles at each point. no cleverness.

If the example pic is indicative of the number of circles and resolution, it shouldnt be a problem for a standard pc

we have 20 circles of average radius 200 so thats approx 20 * 2 π * 200 points * 20 intersection tests = 4800000 iterations

Note:

Iterative approaches like this are flawed in that your step size, in this case the resolution of your output, can greatly affect the result.

Say i have two red circles 2 pixels apart and a 1 pixel radius blue circle to squeeze between them. Clearly with either of the two pixels as the center of the blue circle it will overlap one of the reds. but obviously there is room for the circle if the center lies between the two pixels.

Hence my comment asking about the resolution of the output. which you said could be anything.

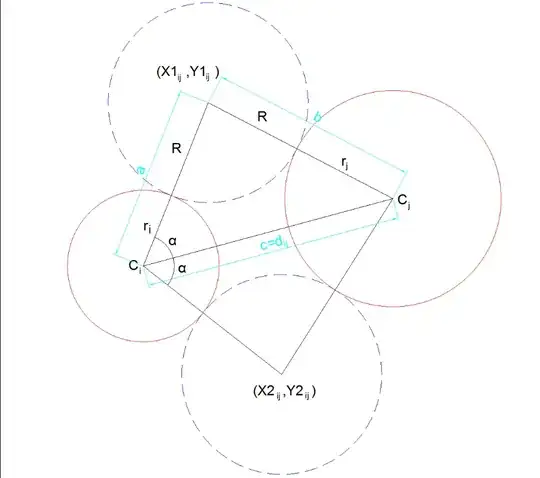
you can also solve the simultaneous equation for each pair of circles with radius increase by the radius of the blue circle.

this will give you the points where the blue circle will touch both red circles more accurately than iterating.

However. there are several conditions where if you only do this you get the wrong or no answer. ie.

1 or no circles

2 or more circles but with target point far away and outside of them.

many circles but with target point close to the surface

Answer 3

This plunk contains working code,

Concept

Given circles are C1, C2 .... Cn

and coordinates of circle Cn is Cnx,Cny and radius is Cr

and radius of required circle is R

if the blue circle is in X,Y location and if it does not conflict with any other circles, following equations are true

(C1x - X)^2 + (C1y - Y)^2 > (C1r + R)^2
(C2x - X)^2 + (C2y - Y)^2 > (C2r + R)^2
....
(Cnx - X)^2 + (Cny - Y)^2 > (Cnr + R)^2

changing first equation,

C1x^2 - 2C1x*X + X^2 + C1y^2 - 2C1y*Y + Y^2 > C1r^2 + 2C1r*R + R^2
X^2 + Y^2 - 2C1x*X - 2C1y*Y > C1r^2 + 2C1r*R + R^2 - C1x^2 - C1y^2

so equations can re-write as,

X^2 + Y^2 - 2C1x*X - 2C1y*Y > C1r^2 + 2C1r*R + R^2 - C1x^2 - C1y^2
X^2 + Y^2 - 2C2x*X - 2C2y*Y > C2r^2 + 2C2r*R + R^2 - C2x^2 - C2y^2
....
X^2 + Y^2 - 2Cnx*X - 2Cny*Y > Cnr^2 + 2Cnr*R + R^2 - Cnx^2 - Cny^2

Implementation

start from the coordinate of the white dot (Xw, Yw),

    var isValidLocation = function(x,y,r){
       var valid = true;
       for (var i = 0; i< circles.length; i++){
          var circle = circles[i];
          valid = valid && ((x*x + y*y - 2*circle.x*x - 2*circle.y*y) > (circle.radius*circle.radius + 2*circle.radius*r + r*r - circle.x*circle.x - circle.y*circle.y));
       }
       return valid;
      };

      var find = function(Xw,Yw,Rw){
        var radius = 0;
        while(true){
          for (var x=-1 * radius ;x <= radius; x++) {
            for (var y=-1 * radius;y <= radius; y++) {
               if (isValidLocation(Xw + x,Yw + y, Rw)){
                 drawCircle(Xw + x,Yw + y,Rw,"#0000FF");
                 return;
               }
            }   
          } 
          radius++;
        }
     }; 

the first coordinate found to satisfy all equations is the location of blue circle

Answer 4

• O being the point that you are trying to be close to

• P being the point that you are looking for (the center of the blue circle

• r being the radius of the blue circle

• C0 .. Cn being the centers of all the circles that restrict placement of the blue on

• extended circle is one of The circles with it radius extended by r

  There is some extra work if O is not at a circle center. So right now assume O == C0

Calculate all the intersections of all the circles with C0, by using their respective radii plus the r, I.e intersect the extend circles with the extended C0. If there are no intersections then the point you are looking for is anywhere on C0, if there are intersections, for each intersection check if it is inside another extended circle (you can limit yourself to the circles that had intersections with C0). Take the first intersection that is not in another extended circle as P, there might be others.

If there are no intersections between the extended circles and C0 that are not inside another extended circle, calculate the intersections of all extended circles with each other. Then check these intersections in order of distance to O, again wether any of the intersections lies within another extended circle, if yes discard, if no that is your result.

If you envision this imagine drawing a line around all the circles that indicate a possible location for your blue circle, taking the union of all of the extended circles will indicate the area your blue circle can't be. The point that you are looking for is the closest point that is not in that union. If there is any point on C0 that is not in that union that is the solution, if C0 is fully covered then P has to be on an intersection between two other extended circles, and it has to be in an area that is not covered by this union (I.e not in an extended circle).

This is O(n^2), there are some ways to improve this though, a gridcan be used to reduce the effort of the pair wise search, also I think sorting the circles by their closeness to O, (the distance between the two circles reduce by the radio) would help to limit the search space for the coverage and intersection search

Answer 5

Possible solutions lookup

1. Check if the white point is the solution by itself. It covers case with 0 red circles and trivial case when red circles are far away from the white point.
2. One red circle.
   1. The white point is the center of the circle. Possible solutions are infinite number of points on the circle with its center in the white point and radius being sum of the blue circles radius and the red circle diameter. Let's call it the green circle.
   2. White point is somewhere else. There is only one possible solution on the line which connects the white point and center of the red circle, it is radius of the blue circle away from the point where the red circle crosses the line towards white point.
3. Two or more red circles.
   1. Let's take red circles one by one and look for possible solution for each of them individually according to point 2 (one circle).
   2. For each pair of the red circles let's check if you can draw the blue circle touching both of the red ones. I.e. if distance between their centers is equal or less than sum of their radiuses plus diameter of the blue circle. If you can then you have two (or one if the red circles are exactly one blue circle diameter away) possible solutions.

---

Actual solution lookup among possible solutions

Now you have a set of points which are possible solutions, iterate through them and check for each.

1. If the point is actually a solution. No red circle should have its center closer than its radius to this point.
2. If it is closer to the white point than solution found before.
3. If you have the green circle (point 2.1)
   • If among individual points there is no solution which belongs to the green circle then the green circle is the answer.
   • If you have individual solutions on the green circle and you need just any solution then just take one of those.
   • If you have individual solutions on the green circle and you need all of the unlimited number of solutions then you need to solve another problem. You need to cut from the green circle all the arcs defined by pair of individual solutions from each red circle.

---

NB: I'm not saying that implementation of the algorithm should be exactly is described. You can try to improve performance using dynamic programming or skipping possible solutions where it is obvious that they won't work.