Should rectangle inherit from square?

Question

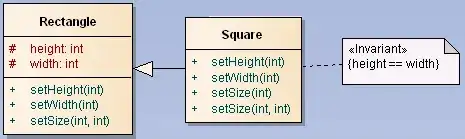
So, we're all probably familiar with the example provided in most textbooks of the Liskov substitution problem involving a square inheriting from rectangle. The objection to this approach is that while a square “is a” rectangle in a mathematical sense, the parent class, rectangle, cannot easily described in terms of a square and thus this model violates one of the fundamental parts of SOLID programming—the Liskov substitution principle.

My question is does it make sense for us to invert the dependency from square "is a" rectangle to rectangle "is a" square. Obviously, in a mathematical setting this is wrong. But a large percentage of why we use OOP is to reduce the amount of, semi unique, code which has to be written, or copy pasted, from place to place. It seems like a relationship between these two structures makes sense, but clearly not the parent child relationship we see in the classical statement of the problem.

I just finished a course on software engineering and I don't think that this point was clearly explained. I know that just because there is an “is a” relationship between two classes does not necessarily imply that there should be any abstraction at all, but it seems satisfying in a mathematical sense for there to be a connection between the two classes.

Also note that I am working on, as a side project, a small game engine and some kind of abstraction between them might make sense.

The thing about squares and rectangles is that they're immutable. The relationship breaks down in these examples because the classes involved are mutable. — Doval, Dec 23 '16 at 17:05
The answer is that (maybe) you should deliberately violate the Liskov substitution principle. Sometimes it makes sense to do so, just as it may make sense on occasion to use a goto or repeat the same code in more than one location. — Ask About Monica, Dec 23 '16 at 18:00
Your question is specifically discussed in the article you linked on Wikipedia. — Paul, Dec 23 '16 at 19:08
@Doval: you surely meant "the relationship breaks down in these examples *if* one makes the decision to design these classes as mutable" - there is no reason why one cannot design them as immutable. — Doc Brown, Dec 23 '16 at 21:29
@DocBrown correct, I phrased it that way because every time the circle/ellipse or rectangle/square problem is brought up the example with the LSP violation has mutable classes. — Doval, Dec 23 '16 at 22:26
In my long career programming, I'd be hard pressed to come up with an example of where LSP ever arose and lack of it caused an issue. Would be interested in learning of real world examples. — user949300, Dec 24 '16 at 05:41
@user949300 Consider an object that is "sent" (by a creator-and-sender) to a "recipient". The sender knows the type precisely, along with its LSP violations if there's any. The recipient doesn't know, merely interacting with that object via an interface. There can be two possible outcomes. The first possibility: the recipient's interaction with the object follows a rigidly-defined scripted response (a "dialogue" or a "play"), which the sender knows perfectly. Thus, the sender knows that the recipient is never exposed to any LSP violation. The second possibility: someone changed the reci ... — rwong, Dec 24 '16 at 09:51
@user949300: (continued) The second possibility: someone came in (junior dev) and changed the recipient's code. Now it is doing something different, although it is still interacting using the interface and the contract it permits. Now the recipient can be exposed to the object's LSP violation. The programmer responsible for the sender sees that something is broken, reprimands the recipient (junior dev) not to change any code. The result is that you have added an "unspoken" contract restriction into the interface, in the name of compatibility. — rwong, Dec 24 '16 at 09:54
@rwong. Those are hypotheticals, illustrating the theory of LSP. I'm asking real world examples from actual code. — user949300, Dec 24 '16 at 15:54
@user949300 I live with the consequences of COM libraries not fully implementing the COM IStream contract. My explanations aren't hypothetical situations. I've seen them all. (In fact my opinion on LSP is largely informed by this experience working with COM IStream.) — rwong, Dec 24 '16 at 17:45
@user949300: Coding by Contract tends to force you to avoid LSP violations. This is primarily an artifact of the fact that contracts provide enforcement of pre-conditions, post-conditions, and invariants (e.g., http://stackoverflow.com/q/7595697/18192 is a real-world example of ). I suppose you could argue that coding by contract is a formalized way of avoiding LSP violations (among other things), so maybe this is a somewhat weak example. Personally, I found the contract validator fighting me every step of the way when I violated LSP (I would call this a feature). — Brian, Dec 29 '16 at 14:43

score 38 · Answer 1 · edited Dec 27 '16 at 16:09

The classic example of square not being able to substitute for rectangle without violating LSP is a bit of a "trick question" and sophistic.

The problem arises because of a conflation... i.e. an implementation of a rectangle is not really a rectangle.

Having independently settable width and height is not an inherent property of a rectangle. A rectangle is still a rectangle even if its width and height are immutable.

Therefore for any given rectangle, it is reasonable that one must not assume anything about constraints (or lack of constraints) on its dimensions. A mathematical rectangle is just that, nothing less, nothing more, and a mathematical square IS in fact a specific perfect example of a mathematical rectangle.

However a rectangle that is guaranteed to have an independently adjustable width and height (as one would normally code behavior in order to make the class useful) is not in fact a rectangle... it is something else. It's a rectangle PLUS certain additional guaranteed behavior.

Therefore this example arises because it creates new things, which are neither rectangles nor squares, but mis-labels them "rectangles" and "squares" and then exclaims "whoa! here's a weird case of some perfect subset violating LSP!". Well that's not the case at all. New things have been created that are neither rectangles nor squares.

To directly answer the OP's question, no it doesn't make sense either mathematically or in computer science to regard a rectangle as a kind of square. I can't see any good reason why one would inherit rectangle from square. Creating methods in that architecture would quickly bear little resemblance/natural mapping to what those words mean to us normally.

Indeed. An immutable ("read-only") `Square` IS-AN immutable `Rectangle`. A "write-only" `Rectangle` (whatever that is and however that may be used) IS-A write-only `Square`. A mutable `Square` and mutable `Rectangle` are neither sub- nor supertypes. — Jörg W Mittag, Dec 24 '16 at 22:45
I guess the "trick" is what the ancient Greek called sophism: "The barber shaves all men in the village who don't shave themselves. Does the barber shave himself?" So here to say: when is a square a rectangle? — , Dec 29 '16 at 12:51

score 7 · Answer 2 · edited Dec 28 '16 at 21:59

7

Liskov's Substitution Principle states that if a program module is using a Base class, then the reference to the Base class can be replaced with a Derived class without affecting the functionality of the program module.

Therefore:

Square cannot inherit from Rectangle.

Imagine the following function, shamelessly copied from Robert C. Martin's Agile Software Development, page 115, The Real Problem:
```
void g(Rectangle& r)
{
    r.SetWidth(5);
    r.SetHeight(4);
    assert(r.Area() == 20);
}
```
One may find it useful to quote the book a few paragraphs below:

One might contend that the problem lays in function g—that the author had no right to make the assumption that width and height were independent. The author of g would disagree. The function g takes a Rectangle as its argument. There are invariants, statements of truth, that obviously apply to a class named Rectangle, and one of those invariants is that height and width are independent. The author of g had every right to assert this invariant. It is the author of Square who has violated the invariant.

Indeed, what happens is that we could imagine a bunch of contracts associated with the rectangle class. Those contracts can be written in code, such as in C# or Java, or be part of the public interface, such as in Eiffel or Spec#, or be only assumed or written in a form of comments.

One of the contracts is suggested by Robert C. Martin and consists of the postcondition of Rectangle::SetWidth(double w):
```
assert((itsWidth == w) && (itsHeight == old.itsHeight));
```
Square violates this postcondition, since itsHeight == old.itsHeight would return false.
Rectangle cannot inherit from Square.

Here, the same logic applies. Imagine that Rectangle inherits now from Square. The function g(Square& s) changes the width of the square, for instance by multiplying it by two. Given the definition of the square, it is wise to assume that the surface area will be multiplied by four.

However, passing an instance of the Rectangle class to g will violate the assumption, since the new surface area will only double instead of quadruple. Same logic applies here, and means that inheriting Rectangle from Square is equally bad.

edited Dec 28 '16 at 21:59

yoniLavi

351
4
8

answered Dec 23 '16 at 17:45

Arseni Mourzenko

134,780
31
343
513

2

Doesn't that just mean your functions are not Liskov-compliant? – Lighthart Dec 23 '16 at 18:23
@Lighthart: no, because they assume things which are true in the context of a base class contract. Take `f(Square s)`. It is perfectly valid to assume for `f` that by multiplying the width by 2, it will quadruple the surface area, because this is the way *all* squares behave. Now if a child class leads the surface to be multiplied by 2 or 1.5 or 100 or to stay the same, it's the fault of the class, not the function. – Arseni Mourzenko Dec 23 '16 at 18:37
3

@ArseniMourzenko I disagree with the assertion that Square cannot inherit from Rectangle. There's nothing stopping class Square from having a method that returns a new *rectangle* with its width multiplied. – Doval Dec 23 '16 at 18:46
3

The assumptions you're making go against the whole reason there are objects in the first place, which is to encapsulate all knowledge about them within their classes. If `Rectangle` has an `area()` method that returns its area, a subclassed `Square` will have one as well that returns the correct value for that shape. Done that way, objects of both classes will be interchangeable if their areas are determined using the defined interface instead of trying to implement expected behavior outside the class. – Blrfl Dec 23 '16 at 19:37
@Doval, Blrfl: looks like I'm a really bad at explaining things today. I edited my answer and included a bunch of quotes and examples from Agile Software Development book. Hope it's better now. – Arseni Mourzenko Dec 23 '16 at 21:08
2

@Arseni I appreciate your efforts but the problem is the example, not a lack of clarity. Rectangles and squares (in mathematics) are immutable values, like numbers. `setWidth` and `setHeight` don't belong on a `Rectangle` Class if you expect it to retain its mathematic properties. When you make the rectangle and square classes immutable the problem goes away and a square can be used everywhere a rectangle can be used. – Doval Dec 23 '16 at 22:40
Now if they were immutable, then square could inherit from rectangle... but they aren't. – Deduplicator Dec 23 '16 at 23:19
The taxonomy here seems to have been designed specifically to create a violation of the LSP in order to say "don't do that." If you're going to assemble a set of classes that behave mostly like rectangles, don't saddle the base class with an invariant that will make it impossible to implement the subclasses you know will be needed. Doubling the width of a plain `Rectangle` doesn't change anything else about it, but `Square` or `RectanlgeWith10to8AspectRatio` can enforce stricter invariants without running afoul of Liskov. – Blrfl Dec 23 '16 at 23:40
1

@Doval *There's nothing stopping class Square from having a method that returns a new rectangle with its width multiplied.* Yes, there is. The assertion of the newly returned object that only either height or width has been changed. A square, no matter whether mutable or immutable, clearly violates the post-condition as it modifies both encapsulated dimensions with a single method call. – Andy Dec 24 '16 at 00:03
@Lighthart The Liskov compliance of functions is precisely what determines the Liskov compliance of the class. – Kevin Krumwiede Dec 24 '16 at 00:08
@Doval "There's nothing stopping class Square from having a method that returns a new rectangle with its width multiplied." - True, but that statement does not imply any inheritance relationship between the classes. – Kevin Krumwiede Dec 24 '16 at 00:08
@Doval If they were immutable, there would be no reason for `Square` to exist as a separate class at all. Squares would simply be instances of `Rectangle` that happen to have the property of their width and height being equal. – Kevin Krumwiede Dec 24 '16 at 00:11
@KevinKrumwiede `If they were immutable, there would be no reason for Square to exist as a separate class at all.` The Square class can enforce that the width and height are equal. A method that accepts a Square doesn't need to check its squareness. A method that accepts a Rectangle does. Immutability lets you encode simple proofs in types. – Doval Dec 24 '16 at 01:05
@Doval: And likewise, a "write-only" `Rectangle` (whatever that is) is a subtype of a write-only `Square`. – Jörg W Mittag Dec 24 '16 at 22:48

Cormac Mulhall · Answer 3 · 2016-12-29T12:53:53.060

5

Object oriented design models behavior, rather than any mathematical properties.

So the short answer is that since a square cannot act like a rectangle and a rectangle doesn't act like a square, they have no child-parent relationship, either way.

The longer answer is a square is a special form of a rectangle only in a specific domain, that being geometric properties. OOD deals with a different domain, modelling behaviour of interacting objects. As such if the relationships are not relevant to this domain you should ignore them. Attempting to model relationships that are actually irrelevant to how the system will behave causes big problems in a system. Stick to the relationships that matter to the behaviour of the system.

edited Dec 29 '16 at 12:53

answered Dec 23 '16 at 17:03

Cormac Mulhall

5,032
2
19
19

14

Well, no. A square is definitely a special form of a rectangle. – Dec 23 '16 at 17:09
There seems to be a wide spread and stuborn misunderstanding about the term "special". In OO a specialisation is typically associated with a descendant. Like a cat is a specialization of an animal, the animal being the general type. This does not apply here at all though. A square is not a specialization of a rectangle. The cat is a specialization of an animal because it has whiskers which animal does not. The square however has nothing over the rectangle, the square is *nothing but* a rectangle. The fact that some people may find the rectangle special (as in remarkable) does not change this. – Martin Maat Dec 27 '16 at 18:20
2

@ThomasKilian A square is a special form of a rectangle only in a specific domain, that being geometric properties. OOD deals with a different domain, modelling behaviour of interacting objects. As such if the relationships are not relevant to this domain you should ignore them. Attempting to model relationships that are actually irrelevant to how the system will behave causes big problems in a system. – Cormac Mulhall Dec 29 '16 at 12:30
Why didn't you write that in your answer? – Dec 29 '16 at 12:47
Didn't think I needed to. But I'll edit the answer to be clearer :-) – Cormac Mulhall Dec 29 '16 at 12:53
That's if we insist on specialization as the foundation of IS-A. What of broadening? "A rectangle is a square with an additional dimension", or less clumsy words to the same effect. – alife Mar 08 '22 at 14:24
It depends but you can quickly run into problems, since a rectangle doesn't simply expand on a square, it has fundamentally different rules. Thus a rectangle can break code that expects a square. One principle of good OO design is that any code that expects a parent class should work just the same if they receive a child of that parent. – Cormac Mulhall Mar 22 '22 at 18:08

score 2 · Answer 4 · 2016-12-27T15:58:32.810

2

Rectangle must not inherit from Square. A square is a special form of a rectangle (where all sides have equal length). So the general form is Rectangle and Square is a specialization. So you can draw a generalization from Square to Rectangle, but not vice versa.

Regarding the Liskov-substitution: if you introduce constraints, you get around the pitfalls. Definitely it's tempting to "just inherit" but of course you still have your brain. And that revealed the problem behind the circle/ellipsis inheritance. So you need to be aware of what you are doing and care for the non-obvious. And: dogmatic programming is not necessarily good programming.

Let's look at a simple design:

Since height/width are protected you need setter methods to alter them. And the constraint on Square will ensure that both height and width must be equal. Now, there can be different implementations for Square. Either a setHeight will as side effect alter the width (which does not seem to be a good idea). Or you raise an exception when trying to do so, which can be implemented in the overrides. As a convenience you can add a setSize with just a single int for height/width which is only available in Square. You can extend this design in similar way with various methods.

edited Dec 27 '16 at 15:58

answered Dec 23 '16 at 17:11

1

But when we draw a generalization from Square to Rectangle there is a violation of the Liskov substitution principal, so there shouldn't be any relationship? Like I say, mathematically, this Rectangle inheriting behaviour from Square is counter intuitive, but most of the same functionality is there and it would not violate the Liskov substitution principal. – ampsthatgoto11 Dec 23 '16 at 17:25
See my added paragraph. – Dec 23 '16 at 17:52
6

*And: dogmatic programming is not necessarily good programming.* Well using inheritance which breaks tests, ie. breaks runtime, is even worse than dogmatic programming. I'd rather have a dogmatic programmer on my team than someone who just slaps an inheritance relationship between a rectangle and a square without even realizing it could violate something (because obviously a square is a special type of a rectangle), and boy it does. – Andy Dec 23 '16 at 17:58
@DavidPacker The above liked duplicate has a nice story for square/rectangle. But basically it's just a bad design that causes the issues. As I said: use your brain! – Dec 23 '16 at 18:04
In the classic example where a `Square` has the property that its X and Y dimensions are equal and a `Rectangle` has the property that they may not be, you cannot generalize in either direction. – Kevin Krumwiede Dec 23 '16 at 20:25
@KevinKrumwiede It simply depends on the operations you provide. And how they respect the constraints put on being the one or the other. In the simple case where the class only offers width/height you can see that you will not run in issues as long as you use setters for width/height. Issues may start with certain operations. – Dec 23 '16 at 22:40
@ThomasKilian If the classes have mutable properties of width and height, then it's plainly obvious that neither `Square` nor `Rectangle` can inherit from the other. Setting the width of a `Square` implies that the height will also be set, which must not be true of a `Rectangle`. Setting the width and height of a `Rectangle` to different values should result in the width and height being different, which must not be true of a `Square`. – Kevin Krumwiede Dec 23 '16 at 23:57
@KevinKrumwiede Didn't I say something about bad design? – Dec 24 '16 at 09:24
@ThomasKilian It's not bad design. You seem to be hung up on the idea that classes called `Square` and `Rectangle` should correspond exactly to the mathematical concepts of the same name, which is not the case in this example. – Kevin Krumwiede Dec 24 '16 at 18:40
@KevinKrumwiede I model something so it has a certain behavior. When I model a generalization like above, it's because I want make use of a generalization, which is **convenient**. I'm not after some dogmatic Liskov and/or building an impossible complete axiomatic system. Good design is useful and correct design. – Dec 24 '16 at 19:03
@ThomasKilian Liskov isn't dogmatic. It's an absolute requirement for good code. – Kevin Krumwiede Dec 24 '16 at 19:08
"I'm pretty sure that nobody can find a flaw in this" Oh well. SetSize is just another rectangle method, slapping it onto square and saying "See, square extends rectangle" is backward. You do not add a method and use that as proof for an inheritence relationship, it is the other way around. Name a trait of square that does not apply to any rectangle and you can start considering inheritence. And no, a constraint is not a trait. – Martin Maat Dec 27 '16 at 06:23

score 2 · Answer 5 · answered Dec 24 '16 at 00:08

Inheritence does not apply at all, either way. Although every square is a rectangle, it does not add anything to the rectangle. It just is a rectangle period, it does not extend rectangle. Inheritence is pointless unless the descendant is (expected) to extend the base class somehow.

The confusion stems from the human label "square" which is totally arbitrary. If people would call a rectangle with long sides twice the length of the short sides a doubie, and the word would be in the English dictionary, you would see the same question about doubies and rectangles on stackexchange.

The same goes for circles and ellipses. Ellipse is the type, circle is just a common incarnation of it.

+1 for "Inheritance does not apply at all". All too often people treat inheritance as a design goal instead of a tool. — Ben Cottrell, Dec 24 '16 at 17:33
Of course you can extend `Square` with new operations. E.g. one that increases height and width the same time. Or one that _squares a circle_. — , Dec 24 '16 at 20:58

score 0 · Answer 6 · answered Dec 24 '16 at 13:02

As you pointed out, it is neither a good idea for Square to inherit from a modifiable Rectangle (any new code in Rectangle could create Squares that are not, well, squares), nor is it a good idea for Rectangle to inherit from Square (the general Rectangle is not a square, so it is a clear violation of the substitutability rule).

The problem must be tackled in another way. Options are:

Make both Square and Rectangle immutable. If the constructor is the only point where the lengths can be set, there is no danger of a Square suddenly becoming a non-square through the use of methods in Rectangle. Also, this helps at implementing strict value semantics, which make code much more readable.
Forget about Square and simply use a Rectangle which just happens to have the same width and height. May be combined with immutability as above, and you might want to add a constructor that takes only a single size argument to construct a Rectangle that happens to be a square.
If you need affine transformations anyway, you can also go the exact opposite route: Have only a square that occupies the rectangle between (0,0) and (1,1), and add an affine transformation to every such square to translate it, stretch it, rotate it, shear it to the precise parallelogram shape you want. Of course, you will have a constructor for axis aligned squares, and one for axis aligned rectangles, but from that point on, you have near absolute freedom. Of course, this is a rather heavy-weight solution, but quite a good one in certain contexts.

Which solution works best for you depends entirely on your use-case. But I've found that it's usually not a bright idea to force something into an inheritance relationship that does not want to be in it. Square and Rectangle are such a pair. Instead, look for solutions that avoid the problem in the first place. That is, what makes a good software developer: The ability to think out of the box, and to come up with creative, simple solutions that fit the current problem at hand easily.

I agree with your basic thoughts, though whether or not generalization from square to rectangle makes sense depends also just on the use case. — , Dec 24 '16 at 21:00

score -4 · Answer 7 · answered Dec 23 '16 at 19:27

I think it can work both ways. You can apply the Strategy Pattern. Although there are not much real life distinct rectangle objects with varying sides.

According to the Strategy Pattern, your square can extend a rectangle - so as it can be correct mathematically. Also, since rectangles and squares all have 4 sides, this should be common for the parent rectangle class. Since the length of the sides are different, you can create an interface <> and have various side lengths implement it. Whereas the Parent rectangle class will be composed of SideLengths instance variables.

I think you can just avoid these complexities and just create separate square and rectangle classes.

Should rectangle inherit from square?

7 Answers7

Linked