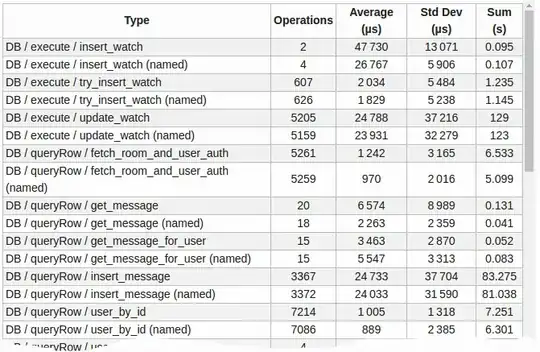
In order to estimate the fastest function in various cases in a non fully deterministic context, I'm running an experiment calling one or the other at random and recording the duration of the operation on the production server.
I get this kind of table:
(numbers grow larger the more I wait)
A problem in interpreting those results is that the standard deviation is big (i.e. various random conditions led to very dispersed durations).
So I'm looking for a way to estimate when the difference between the sample sets is significative or not, some kind of statistical divergence, or, said otherwise, an estimation of the probability the observed difference isn't just random (Shannon theory maybe? Poisson's law?). If it's an accepted best practice or norm, it would be a bonus.
Please keep in mind that I can't keep in memory all samples (right now I just store the number of operation, the sum of durations and the sum of their squares so that I can compute the standard deviation).