7

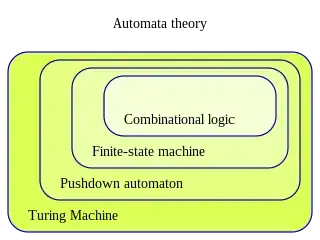
I understand that any language worth its salt can encode a Finite state machine. My question is the opposite, is it possible to convert an arbitrary piece of code ( say in C ) to a functionally equivalent Finite State Machine ?

for example if I have a piece of code with a couple of llvm basic blocks (loops, branches etc), can I replace all of them with a giant state machine, which essentially does the same ?

Jehandad
  • 181
  • 5

3 Answers3

13

The Finite State Machine has less computational power than a Turing machine. That is, the Turing Machine can do things that the FSM cannot. This is true because the FSM is limited in memory by the number of (finite) states.

The following diagram illustrates the relationship between a Finite State Machine and a Turing Machine. As you can see, the Turing Machine is built on top of the other layers, one of which is the Finite State Machine.

Could you write a large enough state machine to encompass any arbitrary piece of code? Possibly. But you won't have a generalized Turing Machine, so there's no guarantee that it's going to work every time.

Automata Theory Venn Diagram

Further Reading

Turing Machine
Finite State Machine

Community
  • 1
Robert Harvey
  • 198,589
  • 55
  • 464
  • 673
  • 1
    I am afraid you do not answer the central question! Which is, can an arbitrary piece of code be converted to an FSM? Difference between state machine types is not under discussion here ! I have edited the question to remove the turing part which might have mislead you, my apologies for that. – Jehandad Apr 18 '16 at 14:38
  • 2
    @Jehandad This does answer the question. C is turing complete and can therefore express things that an FSM cannot. – 8bittree Jul 24 '17 at 22:27
  • 1
    Is it possible to produce a standards-compliant version of C that can *malloc* an infinite amount of memory? – Simon B Jul 25 '17 at 07:46
  • @SimonB Irrelevant. Design an FSM and a Pushdown Automata (PDA) that use all available memory in a given computer, to say recognize all strings consisting of *n* `a`s followed by *n* `b`s. Real world constraints mean that neither implementation can be fully correct, but what happens when you add memory to the computer? The FSM is unaffected, but the PDA can now correctly accept some strings that it incorrectly rejected before. Conversely, if you *remove* memory (within a limit), the FSM will simply not work at all, whereas the PDA will still accept a smaller number of correct strings. – 8bittree Jul 25 '17 at 16:17
  • @8bittree - I think you misunderstand SimonB's point. All C implementations required the size of pointers to objects to have fixed, finite size. This means that for any given implementation of C there exists a memory limit beyond which programs cannot expand even if more memory is added to the computer they are running on. For any such implementation of C, it is possible to produce an FSM with the same behaviour as any program compiled using that implementation. – Jules Jul 20 '18 at 17:58
  • @Jules Unless you reduce the available memory in the actual machine to something more than the minimum the C program requires to run, in which case the C program will continue to run with reduced capability, but the FSM will break entirely. Yes, I might have been hasty in saying that C is turing complete, but I stand by my claim that FSMs are not equivalent. – 8bittree Jul 20 '18 at 18:58
  • @8bittree oh, don't get me wrong. There's no practical application - the fsms for a c implementation with 32 bit pointers would produce O(2^(2^32) ) states, I believe. Its only useful for very small systems (eg microcontroller architectures with 8 bit addresses), and even then is nontrivial. But it's theoretically achievable. – Jules Jul 20 '18 at 19:12
8

Yes, of course it can.

See Bohm & Jacopini's 1966 paper (Yes, fifty years ago), "Flow diagrams, turing machines and languages with only two formation rules" for the gory details.

They showed that any program, even a mess of GOTO-spaghetti, can be converted into a WHILE-loop around a CASE statement, that together implement a finite-state machine.

This was a critical result on the road to Structured Programming. It proved, among other things, that GOTO statements were not necessary.

John R. Strohm
  • 18,043
  • 5
  • 46
  • 56
  • 1
    Did they also prove that the use of unbounded amounts of memory was simultaneously unnecessary? Because if they're still using unbounded memory, then they most certainly do not have a finite-state machine. – 8bittree Jul 24 '17 at 21:28
  • @8bittree: Rather than try to guess what you are really asking and trying to say, I'm going to invite you to read the paper. That's why I gave the citation. – John R. Strohm Jul 24 '17 at 21:37
  • 2
    I would, but it appears to be behind a paywall. Basically, I'm asking if they proved that run time memory allocations are also unneeded. A turing machine can use an infinite amount of memory. An FSM is, by definition, finite. – 8bittree Jul 24 '17 at 21:50
  • @8bittree: As I understand your question, Bohm & Jacopini did not address run-time memory allocation, because that is a function of the application itself, not of the language. – John R. Strohm Jul 24 '17 at 22:38
  • 1
    Then I don't think they've provided sufficient evidence to conclude that all programs can be converted to an FSM. And I'll note that there are formal proofs that prove that there are programs a turing machine can compute, but an FSM cannot. See [here](https://en.wikipedia.org/wiki/Pumping_lemma_for_regular_languages#Use_of_the_lemma) for an example (and note regular languages and FSMs are equivalent). – 8bittree Jul 24 '17 at 23:01
  • 1
    @8bittree - of course, dynamic memory allocation up to a defined limit can be simulate by incrementally using portions of a statically allocated memory block. Real programs run on computers, which tend to have limited memory resources. Actual computers *are* finite state machines (albeit with potentially very large numbers of states). – Jules Apr 12 '18 at 20:49
  • I will grant that an arbitrary Turing machine cannot be converted to a finite state machine, as Robert Harvey's answer points out, but I am not at all certain whether that was the intent of the original question. – John R. Strohm Jun 15 '18 at 17:55
4

No. Consider a piece of code that reads in a string of 0's and recognizes if the string's length is a perfect square (1, 4, 9, 16, 25 ...). Is there a finite state machine that can do this? No, since the set of all such strings is not a regular set (hint: use pumping lemma) and a finite state machine can only recognize a regular set. This example is from page 57 of the book Introduction to automata theory, languages, and computation (1st edition) by Hopcroft and Ullman (available at https://archive.org/details/HopcroftUllman_cinderellabook). Additionally, chapters two and three of this book provide a good introduction to finite state machines, regular sets, and the pumping lemma. There are many other examples of non-regular sets on the Internet. Search for non-regular languages.

Chris Dupilka
  • 41
  • 3
  • 1
    Might want to expand and clarify on regular languages and automata theory; your answer makes perfect sense if you already know these things, which the OP doesn't. – esoterik Jun 15 '18 at 00:58
  • 1
    Is there a C program that does this? (Answer: no. You need infinite memory to recognize strings of unbounded length. Any implementation of C must have a hard memory limit due to finite and fixed pointer sizes.) – Jules Jul 20 '18 at 19:20