1

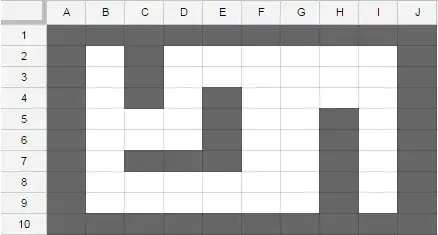
I have a rectangular grid of square tiles, some of which are blocked/filled. I start at a random tile inside the grid with the blocked tiles, randomly placed. I can turn in 90° steps and check whether I can enter the tile in front of me, which is possible if the tile in front of me is not a blocked tile or the edge of the grid. I cannot distinguish both cases from each other, I also have no coordinates and don't "know" my position in the grid.

I now need an algorithm to run through all open tiles of the grid. Using maze-solving algorithms (e.g. Pledge) makes me run along the walls of blocked tiles and the grid's borders, however it is possible that there are free tiles that are not adjacent to a wall, which do not get hit with these algorithms.

What kind of algorithm or logic do I need to use to make sure I cover all empty tiles?

Sample image:

enter image description here

user219317
  • 13
  • 5
  • Would you be able to provide us with an image of the sample grid? Even something basic like an Excel Chart with cells shaded a different color for if they are blocked or not to show your basic problem, like [this](http://imgur.com/D666Dv3) – Rachel Mar 10 '16 at 17:20
  • And as long as your making a sample grid, it would be helpful to see what the desired outcome for that grid would be. Would like you the description of an unblocked path back to your current position or to another position? Is it allowed to use a tile more than once? – Miguel van de Laar Mar 10 '16 at 17:28
  • Do you know the grid size? or maximum dimensions? –  Mar 10 '16 at 18:03
  • I actually find this question interesting. I am assuming this is more of a "room" with a grid interface and randomly placed "objects" in the room, and less of a "maze", and you need an algorithm to traverse every free square in the room from any starting point. Like a Security Guard pathing AI for a randomly generated room. I am guessing that it doesn't matter if the algorithm overlaps anywhere, due to the randomness of it. – Rachel Mar 10 '16 at 18:33

2 Answers2

3

I think you'll want an algorithm something similar to this. The question deals with mapping an unlimited size dynamic "maze", but the solution I think would be the same.

The basic idea is to record each square as you traverse or check it in an array of "known" squares, until you have every square mapped.

  1. Start by recording where you are (0,0) in an array of knownSquares
  2. Pick a direction to move (1,0, 0,1, -1,0, or 0,-1)
  3. Check if new coordinate already exists in array of known squares
    1. If yes, pick the next direction.
      • If no new direction, go back a room
    2. If no, add new coordinate to array of known squares, and check if blocked
      • If blocked, set flag on item in knownSquares that it is blocked and pick a new direction
  4. repeat steps 2-3 until you are out of new squares to visit.

At the end, you should have visited every "square" that was available to the starting spot, and could even graphically display the results of the knownSquares in a UI grid if you wanted to draw the room or verify your results.

Only thing that might cause problems is tracking the order you visit rooms in, but that could easily be solved by a visitOrder property on the object in the knownSquares array, or a separate list altogether if you want a full transcript of each square visited, in order.

Community
  • 1
Rachel
  • 23,979
  • 16
  • 91
  • 159
0

Lets start out by writing a function that interrogates the surrounding walls.

bit field = 0
can move forward?
  if y: bit field |= 1;
rotate R
can move forward?
  if y: bit field |= 2;
rotate R
can move forward?
  if y: bit field |= 4;
rotate R
can move forward?
  if y: bit field |= 8;
rotate R

Now we're pointing back the same way we were and have the bitfield containing something like 0111 or the like. From that we can go forward or to the right or backwards.

So, in an infinite field (or working from known maximum dimensions), put a block to the left and behind us.

  ?
? . ?
X ^ . ?
? . ?
  ?

Now we move into in one of those empty spots. Lets move forward. The new interrogation gives us 1010 and we update the world map.

? X ?
X ^ . ?
X . . ?
? . ?
  ?

So now we place into this data structure the new information about the world.

We move to another location that has adjacent ? and repeat the interrogation of the surroundings and update the world map. If we happen to move into a location that doesn't have any ? adjacent spots, we use our path finding algorithms to go to the nearest . that has an adjacent ?.

When there are no paths to a . that has an adjacent ?, the map of the available world is complete.