Generate equally sized areas in polygon

Question

I am looking for a pseudo code logic that would find n equally sized areas in a given polygon. No space should be between or outside the matched areas. First valid match of areas should be returned.

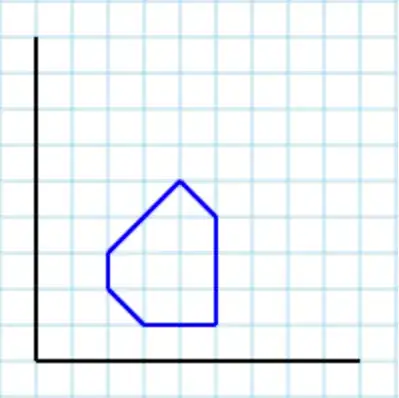
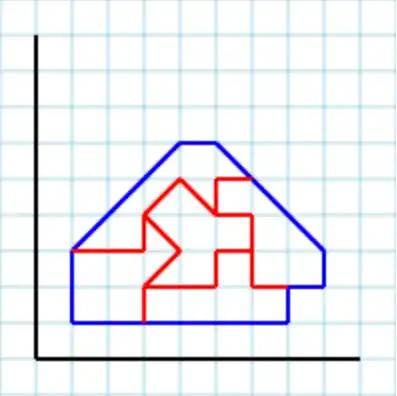
Assuming following polygon [2,2, 3,1, 5,1, 5,4, 4,5, 2,3] as an input:

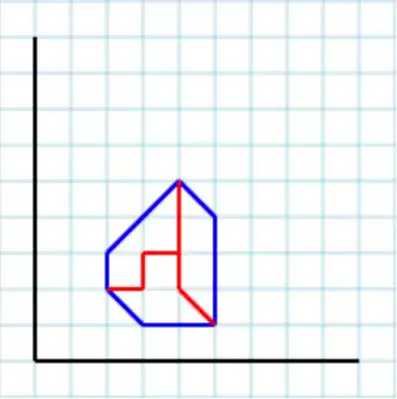
...and 3 as a parameter a valid output could be [ [2,2, 3,2, 3,3, 4,3, 4,5, 2,3], [2,2, 3,1, 5,1, 4,2, 4,3, 3,3, 3,2], [4,5, 4,2, 5,1, 5,4] ]:

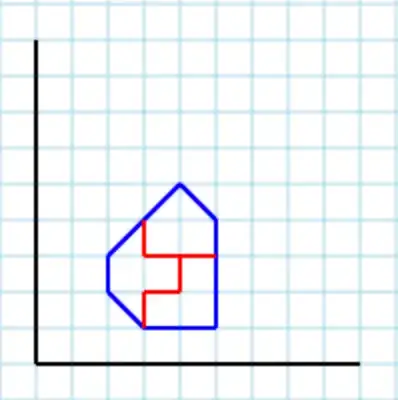
Another valid output with parameter 3 is [ [3,4, 3,3, 4,3, 4,2, 3,2, 3,1, 2,2, 2,3], [4,3, 4,2, 3,2, 3,1, 5,1, 5,3], [3,4, 3,3, 5,3, 5,4, 4,5] ]:

Please note that areas don't have to share same center point. One or more areas may happen to fall right between other areas inside the polygon.

Here is another example of sample input/output.

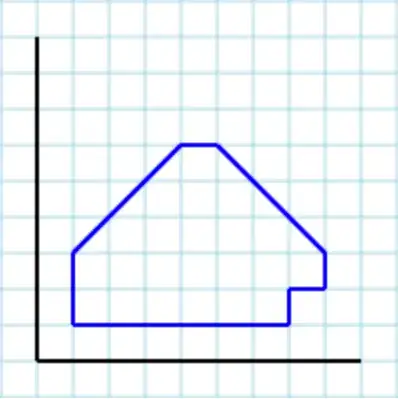
Assuming following polygon [1,3, 1,1, 7,1, 7,2, 8,2, 8,3, 5,6, 4,6] as an input:

..and 5 as a parameter a valid output could be [ [1,3, 1,1, 3,1, 3,2, 4,3, 3,4, 3,3], [3,2, 3,1, 7,1, 7,2, 6,2, 6,3, 5,3, 5,2], [6,2, 8,2, 8,3, 6,5, 5,5, 5,4, 6,4], [1,3, 3,3, 3,4, 5,5, 6,4, 6,5, 7,5, 6,6, 5,6], [3,4, 4,3, 3,2, 5,2, 5,3, 6,3, 6,4, 5,4, 4,5] ]:

Following assumptions are made:

• direction of all borders is divisible by 45

• integer coordinates are used for all polygons

• integer area of input polygon is always divisible by n

• all polygons may be either convex or concave ones

• solvable, meaning n areas can fit properly into the given polygon

Answer 1

Not solvable. I tried a number of methods until i realized it couldn't be done.

Assume a shape with area 4, which should be divided in 2 parts with area 2 each:

The leftmost triangle and square must be part of shape 1, but it needs another triangle. The only place that could be taken from is the square to the right, but then the remainder is split in two regions.

Answer 2

As I said in my comment to Doc Browns (otherwise excellent) answer, there is a matter of choice of square->triangle division which makes it slightly harder to device an algorithm. Also, you don't have to make it serially, but can do it in parallell, as some of my suggestions show.

I made several heuristic approaches at first.

Voronoi: Choose N points (non-integer coordinates) in the shape, create a voronoi map. Let the points attract and repel each other with respect to their area (too large attracts, too small repels).

Useful for large A/N, easy to fall into local maxima.

Circle method: The goal is to remove problematic areas, and then to continue using another method.

Choose a point (non-integer) in the interior, and a radius r. The interior minus the circle will create k disconnected subregions. If any of the subregions are of size A/n, remove it. Also, if any is 2*A/n, it should be easy to split it, and remove them also. Lower the radius slightly, and continue (possibly use some binary search).

Problematic point growth: Begin using the method Doc Brown mentions, but since there are two choices at most edges, skip the graph and grow each region on the border in a way to create as few new problematic points as possible (problematic points=triangles only sharing one edge with the rest of the shape). E.g. when choosing new neighbors to include, add them in order of convexity (concave = negative convexity)

Ribbon growth: For almost convex or convex areas. Choose a point on the exterior edge, make a unit width ribbon follow the exterior edge until it has the right length, making sure to never create a new disconnected point. If necessary, skip the last triangles and make it grow slightly in width. Let the next ribbon follow where the last ended until the final area is of the right size.

Game-like or organic: Create N "countries". Put them in random spots. Let them grow organically. When they meet each other, the one with the smallest current area is the strongest and wins the triangle. Probably prone to local maxima?

Answer 3

The general strategy should be to remove the first piece of area A/n from your polygon P0 (where A is the total area), leaving you with a new polygon P1 of area A-A/n. Then repeat this producing a polygon P2, then P3, and after n repetitions, you have your solution. Note that it is possible at each step that you cannot find such a new piece where the remaining parts still form a connected polygon, in which you have to go back one step and try to find a another piece, or stop the algorithm without a result.

To construct such piece of size A/n, start by dividing up your polygon into "grid pieces". Any grid square inside the polygon forms such a piece, as well as any triangle shaped half-square where the border of the polygon divides the square into two halfs. You can utilize a point-in-polygon test for this, iterate over all half-squares inside the bounding box of the polygon and test if their midpoint is inside the given polygon (if both halfs of a square are contained, one can use the full square instead). Next, you create a planar graph, where each of the pieces define a vertice (with an "area" or "weight" of either 1 or 1/2). The edges of that graph are given by the neighboured pieces. This reduces your geometric problem to a graph problem, where you are looking for a connected sub-graph with vertices of total weight A/n , and the remaining graph is still connected.

The latter problem might be solved by a backtracking approach. Start with one vertice which can be removed from the graph without making it unconnected. You can pick the vertice randomly, if you like, or shuffle the list of all vertices randomly once, for reuse in the following steps. Now try to find a second vertice which is connected to the first one, which can be removed from the remaining graph without destroying its connectedness, too. If there are multiple possibilities, pick one randomly. For vertices representing a square, you can also allow a graph operation where you split up the square into two triangles (this creates new vertices of weight 1/2) by either one or the other possible way. This is only a little bit more complicated than just moving one vertice from the original graph to the sub-graph, but it should not be too difficult at all.

Repeat that until your subgraph reaches a total weight A/n, or you don't find another vertex. If that is the case, "backtrack" one level and try a different vertice first.

There are several ways to optimize this, for example, you have to pick a fast connectivity test for graphs. I guess you will find a lot of algorithms for this sub problem, use Google, or start here. It may be worth looking for an algorithm which can quickly verify if a connected graph is still connected when one vertex is removed.

Hope this helps.