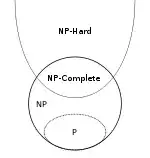
The first thing to understand is that P and NP classify languages, not problems. To understand what this means, we need some other definitions first.
An alphabet is a non-empty finite set of symbols.
{0, 1} is an alphabet as is the ASCII character set. {} is not an alphabet because it is empty. N (the integers) is not an alphabet because it is not finite.
Let Σ be an alphabet. An ordered concatenation of a finite number of symbols from Σ is called a word over Σ.
The string 101 is a word over the alphabet {0, 1}. The empty word (often written as ε) is a word over any alphabet. The string penguin is a word over the alphabet containing the ASCII characters. The decimal notation of the number π is not a word over the alphabet {., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} because it is not finite.
The length of a word w, written as |w|, is the number of symbols in it.
For example, |hello| = 5 and |ε| = 0. For any word w, |w| ∈ N and therefore finite.
Let Σ be an alphabet. The set Σ* contains all words over Σ, including ε. The set Σ+ contains all words over Σ, excluding ε. For n ∈ N, Σn is the set of words of length n.
For every alphabet Σ, Σ* and Σ+ are infinite countable sets. For the ASCII character set ΣASCII, the regular expressions .* and .+ denote ΣASCII* and ΣASCII+ respectively.
{0, 1}7 is the set of 7-bit ASCII codes {0000000, 0000001, …, 1111111}. {0, 1}32 is the set of 32 bit integer values.
Let Σ be an alphabet and L ⊆ Σ*. L is called a language over Σ.
For an alphabet Σ, the empty set and Σ* are trivial languages over Σ. The former is often referred to as the empty language. The empty language {} and the language containing only the empty word {ε} are different.
The subset of {0, 1}32 that corresponds to non-NaN IEEE 754 floating point values is a finite language.
Languages can have an infinite number of words but every language is countable. The set of strings {1, 2, …} denoting the integers in decimal notation is an infinite language over the alphabet {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. The infinite set of strings {2, 3, 5, 7, 11, 13, …} denoting the prime numbers in decimal notation is a proper subset thereof. The language containing all words matching the regular expression [+-]?\d+\.\d*([eE][+-]?\d+)? is a language over the ASCII character set (denoting a subset of the valid floating-point expressions as defined by the C programming language).
There is no language containing all real numbers (in any notation) because the set of real numbers is not countable.
Let Σ be an alphabet and L ⊆ Σ*. A machine D decides L if for every input w ∈ Σ* it computes the characteristic function χL(w) in finite time. The characteristic function is defined as
χL: Σ* → {0, 1}
w ↦ 1, w ∈ L
0, otherwise.
Such a machine is called a decider for L. We write “D(w) = x” for “given w, D outputs x”.
There are many machine models. The most general one that is in practical use today is the model of a Turing machine. A Turing machine has unlimited linear storage clustered into cells. Each cell can hold exactly one symbol of an alphabet at any point in time. The Turing machine performs its computation as a sequence of computation steps. In each step, it can read one cell, possibly overwrite its value and move the read/write head by one position to the left or right cell. What action the machine will perform is controlled by a finite state automaton.
A random access machine with a finite set of instructions and unlimited storage is another machine model that is as powerful as the Turing machine model.
For the sake of this discussion, we shall not bother us with the precise machine model we use but rather suffice to say that the machine has a finite deterministic control unit, unlimited storage and performs a computation as a sequence of steps that can be counted.
Since you've used it in your question, I assume that you're already familiar with “big-O” notation so here is only a quick refresher.
Let f: N → be a function. The set O(f) contains all functions g: N → N for which there exist constants n0 ∈ N and c ∈ N such that for every n ∈ N with n > n0 it is true that g(n) ≤ c f(n).
Now we are prepared to approach the real question.
The class P contains all languages L for which there exists a Turing machine D that decides L and a constant k ∈ N such that for every input w, D halts after at most T(|w|) steps for a function T ∈ O(n ↦ nk).
Since O(n ↦ nk), while mathematically correct, is inconvenient to write and read, most people – to be honest, everybody except myself – usually writes simply O(nk).
Note that the bound depends on the length of w. Therefore, the argument you make for the language of the primes is only correct for numbers in unaray encodings, where for the encoding w of a number n, the length of the encoding |w| is proportional to n. Nobody would ever use such an encoding in practice. Using a more advanced algorithm than simply trying all possible factors, it can be shown, however, that the language of prime numbers remains in P if the inputs are encoded in binary (or to any other base). (Despite massive interest, this could only be proven by Manindra Agrawal, Neeraj Kayal, and Nitin Saxena in an award-winning paper in 2004 so you can guess that the algorithm is not very simple.)
The trivial languages {} and Σ* and the non-trivial language {ε} are obviously in P (for any alphabet Σ). Can you write functions in your favorite programming language that take a string as input and return a boolean telling whether the string is a word from the language for each of these and prove that your function has polynomial run-time complexity?
Every regular language (a language described by a regular expression) is in P.
Let Σ be an alphabet and L ⊆ Σ*. A machine V that takes an encoded tuple of two words w, c ∈ Σ* and outputs 0 or 1 after a finite number of steps is a verifier for L if it has the following properties.
- Given (w, c), V outputs 1 only if w ∈ L.
- For every w ∈ L, there exists a c ∈ Σ* such that V(w, c) = 1.
The c in the above definition is called a witness (or certificate).
A verifier is allowed to give false negatives for the wrong witness even if w actually is in L. It is not, however, allowed to give false positives. It is also required that for each word in the language, there exists at least one witness.
For the language COMPOSITE, that contains the decimal encodings of all integers that are not prime, a witness could be a factorization. For example, (659, 709) is a witness for 467231 ∈ COMPOSITE. You can easily verify that on a sheet of paper while without the witness given, proving that 467231 is not prime would be difficult without using a computer.
We didn't say anything about how an appropriate witness can be found. This is the non-deterministic part.
The class NP contains all languages L for which there exists a Turing machine V that verifies L and a constant k ∈ N such that for every input (w, c), V halts after at most T(|w|) steps for a function T ∈ O(n ↦ nk).
Note that the above definition implies that for each w ∈ L there exists a witness c with |c| ≤ T(|w|). (The Turing machine cannot possibly look at more symbols of the witness.)
NP is a superset of P (why?). It is not known whether there exist languages that are in NP but not in P.
Integer factorization is not a language per se. However, we can construct a language that represents the decision problem associated with it. That is, a language that contains all tuples (n, m) such that n has a factor d with d ≤ m. Let us call this language FACTOR. If you have an algorithm to decide FACTOR, it can be used to compute a full factorization with only polynomial overhead by performing a recursive binary search for each prime factor.
It is easy to show that FACTOR is in NP. An appropriate witness would simply be the factor d itself and all the verifier would have to do is verify that d ≤ m and n mod d = 0. All of this can be done in polynomial time. (Remember, again, that it is the length of the encoding that counts and that is logarithmic in n.)
If you can show that FACTOR is also in P, you can be sure to get many cool awards. (And you have broken a significant portion of today's cryptography.)
For every language in NP, there is a brute-force algorithm that decides it deterministically. It simply performs an exhaustive search over all witnesses. (Note that the maximum length of a witness is bounded by a polynomial.) So, your algorithm to decide PRIMES was actually a brute-force algorithm to decide COMPOSITE.
To address your final question, we need to introduce reduction. Reductions are a very powerful concept of theoretical computer science. Reducing one problem to another basically means solving one problem by means of solving another problem.
Let Σ be an alphabet and A and B be languages over Σ. A is polynomial-time many-one reducible to B if there exists a function f: Σ* → Σ* with the following properties.
- w ∈ A ⇔ f(w) ∈ B for all w ∈ Σ*.
- The function f can be computed by a Turing machine for every input w in a number of steps bounded by a polynomial in |w|.
In this case, we write A ≤p B.
For example, let A be the language that contains all graphs (encoded as adjacency matrix) that contain a triangle. (A triangle is a cycle of length 3.) Let further B be the language that contains all matrices with non-zero trace. (The trace of a matrix is the sum of its main diagonal elements.) Then A is polynomial-time many-one reducible to B. To prove this, we need to find an appropriate transformation function f. In this case, we can set f to compute the 3rd power of the adjacency matrix. This requires two matrix-matrix products, each of which has polynomial complexity.
It is trivially true that L ≤p L. (Can you prove it formally?)
We'll apply this to NP now.
A language L is NP-hard if and only if L' ≤p L for every language L' ∈ NP.
An NP-hard language may or may not be in NP itself.
A language L is NP-complete if and only if
The most famous NP-complete language is SAT. It contains all boolean formulas that can be satisfied. For example, (a ∨ b) ∧ (¬a ∨ ¬b) ∈ SAT. A valid witness is {a = 1, b = 0}. The formula (a ∨ b) ∧ (¬a ∨ b) ∧ ¬b ∉ SAT. (How would you prove that?)
It is not difficult to show that SAT ∈ NP. To show the NP-hardness of SAT is some work but it was done in 1971 by Stephen Cook.
Once that one NP-complete language was known, it was relatively simple to show the NP-completeness of other languages via reduction. If language A is known to be NP-hard, then showing that A ≤p B shows that B is NP-hard, too (via the transitivity of “≤p”). In 1972 Richard Karp published a list of 21 languages that he could show were NP-complete via (transitive) reduction of SAT. (This is the only paper in this answer that I actually recommend you should read. Unlike the others, it is not hard to understand and gives a very good idea of how proving NP-completeness via reduction works.)
Finally, a short summary. We'll use the symbols NPH and NPC to denote the classes of NP-hard and NP-complete languages respectively.
- P ⊆ NP
- NPC ⊂ NP and NPC ⊂ NPH, actually NPC = NP ∩ NPH by definition
- (A ∈ NP) ∧ (B ∈ NPH) ⇒ A ≤p B
Note that the inclusion NPC ⊂ NP is proper even in the case that P = NP. To see this, make yourself clear that no non-trivial language can be reduced to a trivial one and there are trivial languages in P as well as non-trivial languages in NP. This is a (not very interesting) corner-case, though.
Addendum
Your primary source of confusion seems to be that you were thinking of the “n” in “O(n ↦ f(n))” as the interpretation of an algorithm's input when it actually refers to the length of the input. This is an important distinction because it means that the asymptotic complexity of an algorithm depends on the encoding used for the input.
This week, a new record for the largest known Mersenne prime was achieved. The largest currently known prime number is 274 207 281 − 1. This number is so huge that it gives me a headache so I'll use a smaller one in the following example: 231 – 1 = 2 147 483 647. It can be encoded in different ways.
- by its Mersenne exponent as decimal number:
31 (2 bytes)
- as decimal number:
2147483647 (10 bytes)
- as unary number:
11111…11 where the … is to be replaced by 2 147 483 640 more 1s (almost 2 GiB)
All these strings encode the same number and given any of these, we can easily construct any other encoding of the same number. (You can replace decimal encoding with binary, octal or hexadecimal if you want to. It only changes the length by a constant factor.)
The naive algorithm for testing primality is only polynomial for unary encodings. The AKS primality test is polynomial for decimal (or any other base b ≥ 2). The Lucas-Lehmer primality test is the best known algorithm for Mersenne primes Mp with p an odd prime but it is still exponential in the length of the binary encoding of the Mersenne exponent p (polynomial in p).
If we want to talk about the complexity of an algorithm, it is very important that we are very clear what representation we use. In general, one can assume that the most efficient encoding is used. That is, binary for integers. (Note that not every prime number is a Mersenne prime so using the Mersenne exponent is not a general encoding scheme.)
In theoretical cryptography, many algorithms are formally passed a completely useless string of k 1s as the first parameter. The algorithm never looks at this parameter but it allows it to formally be polynomial in k, which is the security parameter used to tune the security of the procedure.
For some problems for which the decision language in binary encoding is NP-complete, the decision language is no longer NP-complete if the encoding of embedded numbers is switched to unary. The decision languages for other problems remain NP-complete even then. The latter are called strongly NP-complete. The best known example is bin packing.
It is also (and perhaps more) interesting to see how the complexity of an algorithm changes if the input is compressed. For the example of Mersenne primes, we have seen three encodings, each of which is logarithmically more compressed than its predecessor.
In 1983, Hana Galperin and Avi Wigderson have written an interesting paper about the complexity of common graph algorithms when the input encoding of the graph is compressed logarithmically. For these inputs, the language of graphs containing a triangle from above (where it was clearly in P) suddenly becomes NP-complete.
And that's because language classes like P and NP are defined for languages, not for problems.