Sorry for the poor title but I didn't have a better way to phrase it...
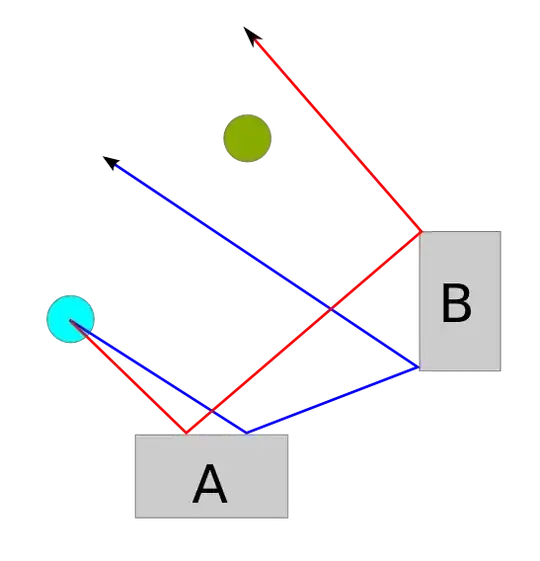
So there's this amazing game by Nintendo (yes!) on Wii called WiiPlay. There're 9 minigames in it, and my favorite one is called Tanks!. It's about destroying COM enemy tanks without getting yourself destroyed. Here's a screenshot of a level:
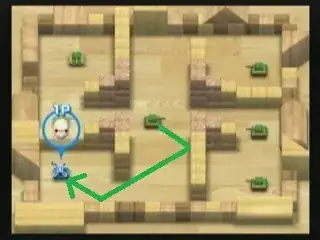
One way to destroy tanks is by firing bullets. There's this lime green enemy tank which fires high-speed bullets that ricochet (against the walls and blocks) twice. You can see how the player tank can get instantly destroyed if it stays at where it is now, as that lime tank in the center can fire a bullet that follows the green path I drew on the image.
As an amateur programmer myself I have been wondering how can the lime tank determine at which direction it should fire at to smite the player tank.
I thought about it myself but didn't came up with any possible algorithm. I'll explain my conclusions in case they inspire someone. Just for simplicity during my explanation, I assume a wall to be any surface against which a bullet can ricochet. An isolated rectangle of blocks thusly form four walls.
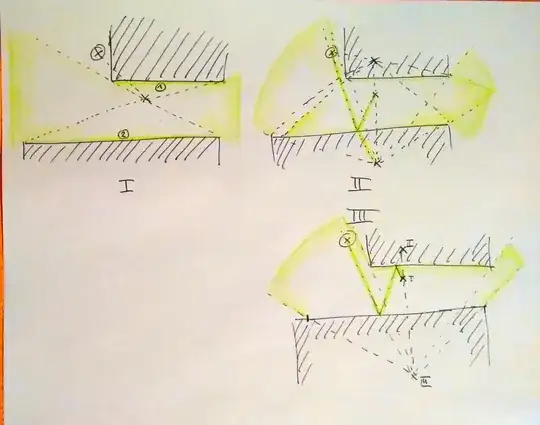
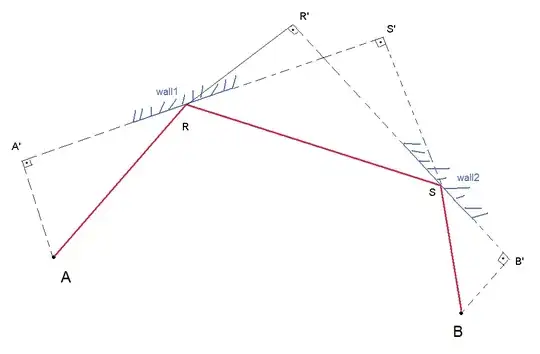
I concluded that the 2 points at which the bullet ricochets always either lie on one side of a parallelogram or become opposite vertices of a parallelogram. The firing enemy tank and the player tank it aims are not necessarily the other 2 vertices but definitely lie on the lines colinear to either of the four sides of the parallelogram. Here is an illustration of the 4 possible ways a parallelogram can be formed:

HOR-VER means the bullet first hits a horizontal wall, then it hits a vertical wall.
And then I'm stuck. I thought about moving around a line that connects the enemy tank and the player tank around the map to see if it forms a parallelogram with any two hits with any wall, but this does not always work because the enemy tank and the player tank are not necessarily coincidental with the vertices of the parallelogram.
Also, I'm not sure of the general flow of the algorithm. Does the algorithm take any of the following 2 structures, or maybe I am wrong with both of these?
- Keep figuring out possible paths and always mark one as the best (can be the shortest, the most obscure, the most inescapable, or a combined and weighted assessment based on multiple criteria) and forget about the rest. The one left after all calculation is the best one to take.
- First determine all walls first reachable with the bullet (the bullet needs not ricochet against any other wall in order to reach each of these walls), then determine all reachable ranges on each of these walls (it is sometimes impossible to reach a faraway point on a wall without ricochet if another wall stands near you), then again determine all reachable walls with a ricochet, and all ranges reachable on these walls. These 4 processes can be done by a way similar to ray-tracing. During each process, if the player tank is hit by any ray, figure out the bullet path according to that ray.
In my opinion, this algorithm is hard to figure out because:
- a bullet can be fired in any direction; and
- there are infinitely many points on any wall, as in mathematics, where there are infinitely many points on a line.
But Nintendo people made it anyway, so... anybody with an idea?