Algorithm to solve this "treefarm" puzzle

Question

How would I go about writing a program to solve this kind of puzzle: The green squares represent trees, and you have to plant them in such a way, so that:

• Trees do not touch each other at all (not even diagonally)
• Each row and column contain a specific number of trees, which is denoted in the corresponding cell to the right of or below the main grid respectively

The numbers within cells of the main grid are irrelevant.

I can immediately eliminate rows and columns with a required tree amount of 1 that have a tree in them, and 9x9 squares around each of the trees. After that, I got stuck.

Thanks for any ideas.

Answer 1

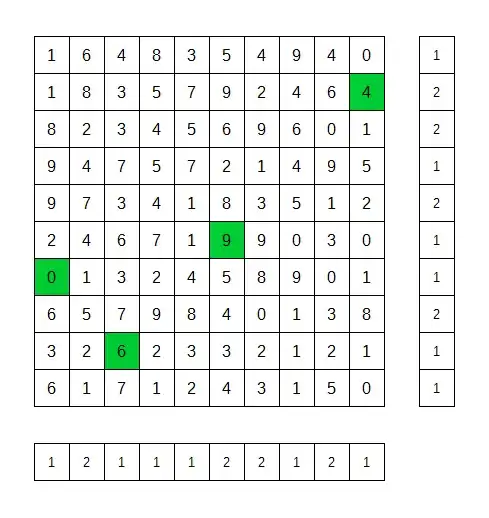
When solving a puzzle like this, there are two things you can do:

1. Look for places where you can apply some pattern to cross out a square or plant a tree there with certainty
2. Make a guess, and proceed until it either comes to an unsolveable situation (in which case you backtrack to your previous guess), or you finish.

---

For this particular puzzle, the operations falling into the first category that I can see would be:

• Mark off all cells in rows or columns containing an equal number of trees to the number required (including 0).
• Mark off all cells adjacent to a planted tree
• In any row or column with only one remaining cell and one more tree required, plant a tree in that cell
• In any row or column with two remaining cells and two more trees required, plant a tree in both of those cells
• In any row or column with three remaining cells which are all connected, and two more trees required, plant a tree in the cells at either end of the group of three.
• In any row or column with three remaining cells where two are connected, and two more trees required, plant a tree in the disconnected cell.

These all need to be checked for every row, column and tree when first starting. After that, the first two can be done immediately when planting a tree.

If row and column numbers greater than 2 are allowed you'll have to work out a more general version of the final 4 rules. Alternatively, a simple brute force which checks all valid combinations to see if any of them either always have a tree or never have a tree would work.

---

For the second category, you're going to be doing a depth-first tree search. For each node, you'll want to do the following:

1. If this is a leaf node, check if it's terminal (the game is unwinnable or won). If so, either you're done or you need to backtrack up to the parent
2. If this is a leaf node, apply the identities above to see if you can instantly mark off or plant trees in any more tiles.
3. If this is a leaf node, add children corresponding to some unfilled tiles which are not marked off.
4. Pick a child which has not already been fully expanded, and expand it.

A naive method for 3. and 4. would be to add all unmarked children, then pick one at random (or in an arbitrary order) to expand. But you can almost certainly do better with a heuristic.

One that springs immediately to mind is for the third step, pick the row or column with the least possible combinations of tree placements satisfying it in isolation. For example, the fifth row from the top has five possible combinations satisfying it. Then only add one child for each of these combinations. You know that one of them will definitely be correct, so you now only have 5 children to expand, one of which will for sure get to the right answer.

Answer 2

This looks like variation of nonogram puzzle. You can find some inspiration from existing nonogram solvers. It seems that you would need to add constraint about boxes not touching diagonally.