After fidgeting around with the code a bit, I've got some better results. I went back to the original paper and ignored the wikipedia page. I've compared the algorithm to other quick select routines with some great results.
Ok, here are the methods I have been playing with. Note these are for floating point and also that I changed my method from a void.
Quick Select ver 1
float quickselect(float *arr, int length, int kTHvalue)
{
#define F_SWAP(a, b) { tmp = arr[a]; arr[a] = arr[b]; arr[b] = tmp; }
int i, st;
float tmp;
for (st = i = 0; i < length - 1; i++)
{
if (arr[i] > arr[length-1]) continue;
F_SWAP(i, st);
st++;
}
F_SWAP(length-1, st);
#undef F_SWAP
return kTHvalue == st ?arr[st]
:st > kTHvalue ? quickselect(arr, st, kTHvalue)
: quickselect(arr + st, length - st, kTHvalue - st);
}
I think the original source is Rosetta code. It works rather quickly, but after looking at some other codes, another quick select function was written.
Quick Select ver 2
float quickselect2(float *arr, int length, int kthLargest)
{
#define F_SWAP(a, b) { tmp = a; a = b; b = tmp; }
int left = 0;
int right = length - 1;
int pos;
float tmp;
for (int j = left; j < right; j++)
{
float pivot = arr[kthLargest];
F_SWAP(arr[kthLargest], arr[right]);
for (int i = pos = left; i < right; i++)
{
if (arr[i] < pivot)
{
F_SWAP(arr[i], arr[pos]);
pos++;
}
}
F_SWAP(arr[right], arr[pos]);
#undef F_SWAP
if (pos == kthLargest) break;
if (pos < kthLargest) left = pos + 1;
else right = pos - 1;
}
return arr[kthLargest];
}
I looked around and found yet another quick select that had some good promise. It was a quick select with a Median of 3
float quickselect_MO3(float *arr, const int length, const int kTHvalue)
{
#define F_SWAP(a,b) { float temp=(a);(a)=(b);(b)=temp; }
unsigned int low = 0;
unsigned int high = length - 1;
for (unsigned int j = low; j < high; j++)
{
if (high <= low) // One element only
return arr[kTHvalue];
if (high == low + 1)
{ // Two elements only
if (arr[low] > arr[high])
F_SWAP(arr[low], arr[high]);
return arr[kTHvalue];
}
//median of 3
int middle = (low + high) / 2;
if (arr[middle] > arr[high])
F_SWAP(arr[middle], arr[high]);
if (arr[low] > arr[high])
F_SWAP(arr[low], arr[high]);
if (arr[middle] > arr[low])
F_SWAP(arr[middle], arr[low]);
// Swap low item (now in position middle) into position (low+1)
F_SWAP(arr[middle], arr[low+1]);
// Nibble from each end towards middle, swapping items when stuck
unsigned int ll = low + 1;
unsigned int hh = high - 1;//unsigned int hh = high;
for (unsigned int k = ll; k < hh; k++)
{
do ll++; while (arr[low] > arr[ll]);
do hh--; while (arr[hh] > arr[low]);
if (hh < ll)
break;
F_SWAP(arr[ll], arr[hh]);
}
// Swap middle item (in position low) back into correct position
F_SWAP(arr[low], arr[hh]);
// Re-set active partition
if (hh <= kTHvalue)
low = ll;
if (hh >= kTHvalue)
high = hh - 1;
}
#undef F_SWAP
}
The Median of 3 is fast and rather impressive.
Next, with my rewritten (from the original ALGOL converted in the paper) Floyd Routine.
the Floyd median function ver 1
float select(float array[], int left, int right, int k)
{
#define sign(x) ((x > 0.0) ? 1 : ((x < 0.0) ? (-1) : 0))
#define F_SWAP(a,b) { float temp=(a);(a)=(b);(b)=temp; }
int i;
right = right - 1;
while (right > left)
{
// use select recursively to sample a smaller set of size s
// the arbitrary constants 600 and 0.5 are used in the original
// version to minimize execution time
if (right - left > right)
{
int n = right - left + 1;
i = k - left + 1;
float z = logf(n);
float s = 0.5 * expf(2 * z/3);
float sd = 0.5 * sqrtf(z * s * (n - s) / n) * sign(i - n / 2);
int ll = max(left, k - 1 * s/n + sd);
int rr = min(right, k + (n - 1) * s/n + sd);
select(array, ll, rr, k);
}
// partition the elements between left and right around t
float t = array[k];
i = left;
int j = right;
F_SWAP(array[left],array[k]);
if (array[right] > t)
{
F_SWAP(array[right],array[left]);
}
while (i < j)
{
F_SWAP(array[i],array[j]);
i++;
j--;
while (array[i] < t)
{
i++;
}
while (array[j] > t)
{
j--;
}
}
if (array[left] == t)
{
F_SWAP (array[left], array[j])
}
else
{
j++;
F_SWAP (array[j],array[right])
}
// adjust left and right towards the boundaries of the subset
// containing the (k - left + 1)th smallest element
if (j <= k)
{
left = j + 1;
}
if (k <= j)
{
right = j - 1;
}
}
return array[k];
#undef sign
#undef F_SWAP
}
Finally, I decided to remove the Log function, Exponent and square root functions and got the same output and even a better time.
the Floyd median function ver 2
float select1(float array[], int left, int right, int k)
{
#define sign(x) ((x > 0.0) ? 1 : ((x < 0.0) ? (-1) : 0))
#define F_SWAP(a,b) { float temp=(a);(a)=(b);(b)=temp; }
int i;
right = right - 1;
while (right > left)
{
// use select recursively to sample a smaller set of size s
// the arbitrary constants 600 and 0.5 are used in the original
// version to minimize execution time
if (right - left > right)
{
int n = right - left + 1;
i = k - left + 1;
int s = (2 * n / 3);
int sd = (n * s * (n - s) / n) * sign(i - n / 2);
int ll = max(left, k - i * s / n + sd);
int rr = min(right, k + (n - i) * s / n + sd);
select1(array, ll, rr, k);
}
// partition the elements between left and right around t
float t = array[k];
i = left;
int j = right;
F_SWAP(array[left],array[k]);
if (array[right] > t)
{
F_SWAP(array[right],array[left]);
}
while (i < j)
{
F_SWAP(array[i],array[j]);
i++;
j--;
while (array[i] < t)
{
i++;
}
while (array[j] > t)
{
j--;
}
}
if (array[left] == t)
{
F_SWAP (array[left], array[j])
}
else
{
j++;
F_SWAP (array[j],array[right])
}
// adjust left and right towards the boundaries of the subset
// containing the (k - left + 1)th smallest element
if (j <= k)
{
left = j + 1;
}
if (k <= j)
{
right = j - 1;
}
}
return array[k];
#undef sign
#undef F_SWAP
}
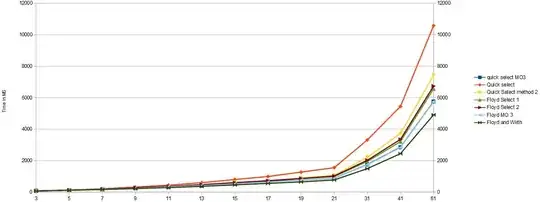
Here is a chart of the results
EDIT
I coded the Floyd Routine with the median of 3 and updated the chart. It rates about the same speed as quick select with Median of 3, slightly slower. It deserves a little more exploration.
float select3(float array[], int left, int right, int k)
{
#define sign(x) ((x > 0.0) ? 1 : ((x < 0.0) ? (-1) : 0))
#define F_SWAP(a,b) { float temp=(a);(a)=(b);(b)=temp; }
int i;
right = right - 1;
while (right > left)
{
if( array[k] < array[left] ) F_SWAP(array[left],array[k]);
if( array[right] < array[left] ) F_SWAP(array[left],array[right]);
if( array[right] < array[k] ) F_SWAP(array[k],array[right]);
if (right - left > right)
{
int n = right - left + 1;
i = k - left + 1;
int s = (2 * n / 3);
int sd = (n * s * (n - s) / n) * sign(i - n / 2);
int ll = max(left, k - i * s / n + sd);
int rr = min(right, k + (n - i) * s / n + sd);
select1(array, ll, rr, k);
}
// partition the elements between left and right around t
float t = array[k];
i = left;
int j = right;
F_SWAP(array[left],array[k]);
if (array[right] > t)
{
F_SWAP(array[right],array[left]);
}
while (i < j)
{
F_SWAP(array[i],array[j]);
i++;
j--;
while (array[i] < t)
{
i++;
}
while (array[j] > t)
{
j--;
}
}
if (array[left] == t)
{
F_SWAP (array[left], array[j])
}
else
{
j++;
F_SWAP (array[j],array[right])
}
// adjust left and right towards the boundaries of the subset
// containing the (k - left + 1)th smallest element
if (j <= k)
{
left = j + 1;
}
if (k <= j)
{
right = j - 1;
}
}
return array[k];
#undef sign
#undef F_SWAP
}
As you can see, the Floyd routine is faster than any of the quick selects other than the version with the median of 3. I don't see why the median of 3 could not be added to the Floyd routine and I will look at that next. As for the Floyd routine, of course removing the floating point log, exp and sqrt functions speeds up the routine.
I still haven't figured out why Floyd put it there in the first place.
edit 6-7-15
Here is the non-recursive version, runs at the same speed as the recursive version.
float select7MO3(float array[], const int length, const int kTHvalue)
{
#define sign(x) ((x > 0) ? 1 : ((x < 0) ? (-1) : 0))
#define F_SWAP(a,b) { float temp=(a);(a)=(b);(b)=temp; }
int left = 0;
int i;
int right = length - 1;
int rr = right;
int ll = left;
while (right > left)
{
if( array[kTHvalue] < array[left] ) F_SWAP(array[left],array[kTHvalue]);
if( array[right] < array[left] ) F_SWAP(array[left],array[right]);
if( array[right] < array[kTHvalue] ) F_SWAP(array[kTHvalue],array[right]);
if ((right - left) > kTHvalue)
{
int n = right - left + 1;
i = kTHvalue - left + 1;
int s = (2 * n / 3);
int sd = (n * s * (n - s) / n) * sign(i - n);
ll = max(left, kTHvalue - i * s / n + sd);
rr = min(right, kTHvalue + (n - i) * s / n + sd);
}
// partition the elements between left and right around t
float t = array[kTHvalue];
i = left;
int j = right;
F_SWAP(array[left],array[kTHvalue]);
if (array[right] > t)
{
F_SWAP(array[right],array[left]);
}
while (i < j)
{
F_SWAP(array[i],array[j]);
i++;
j--;
while (array[i] < t)
{
i++;
}
while (array[j] > t)
{
j--;
}
}
if (array[left] == t)
{
i--;
F_SWAP (array[left], array[j])
}
else
{
j++;
F_SWAP (array[j],array[right])
}
// adjust left and right towards the boundaries of the subset
// containing the (k - left + 1)th smallest element
if (j <= kTHvalue)
{
left = j + 1;
}
else if (kTHvalue <= j)
{
right = j - 1;
}
}
return array[kTHvalue];
#undef sign
#undef F_SWAP
}
edit 6-13-15
I experimented some more with the Floyd selection routine and started to compare his routine against N. Wirth selection routine. An idea came across, what would happen if I combined his routine with Floyd's routine. This is what I came up with.
float FloydWirth_kth(float arr[], const int length, const int kTHvalue)
{
#define F_SWAP(a,b) { float temp=(a);(a)=(b);(b)=temp; }
#define SIGNUM(x) ((x) < 0 ? -1 : ((x) > 0 ? 1 : (x)))
int left = 0;
int right = length - 1;
int left2 = 0;
int right2 = length - 1;
//while (left < right)
while (left < right)
{
if( arr[right2] < arr[left2] ) F_SWAP(arr[left2],arr[right2]);
if( arr[right2] < arr[kTHvalue] ) F_SWAP(arr[kTHvalue],arr[right2]);
if( arr[kTHvalue] < arr[left2] ) F_SWAP(arr[left2],arr[kTHvalue]);
int rightleft = right - left;
if (rightleft < kTHvalue)
{
int n = right - left + 1;
int ii = kTHvalue - left + 1;
int s = (n + n) / 3;
int sd = (n * s * (n - s) / n) * SIGNUM(ii - n / 2);
int left2 = max(left, kTHvalue - ii * s / n + sd);
int right2 = min(right, kTHvalue + (n - ii) * s / n + sd);
}
float x=arr[kTHvalue];
while ((right2 > kTHvalue) && (left2 < kTHvalue))
{
do
{
left2++;
}while (arr[left2] < x);
do
{
right2--;
}while (arr[right2] > x);
//F_SWAP(arr[left2],arr[right2]);
F_SWAP(arr[left2],arr[right2]);
}
left2++;
right2--;
if (right2 < kTHvalue)
{
while (arr[left2]<x)
{
left2++;
}
left = left2;
right2 = right;
}
if (kTHvalue < left2)
{
while (x < arr[right2])
{
right2--;
}
right = right2;
left2 = left;
}
if( arr[left] < arr[right] ) F_SWAP(arr[right],arr[left]);
}
#undef F_SWAP
#undef SIGNUM
return arr[kTHvalue];
}
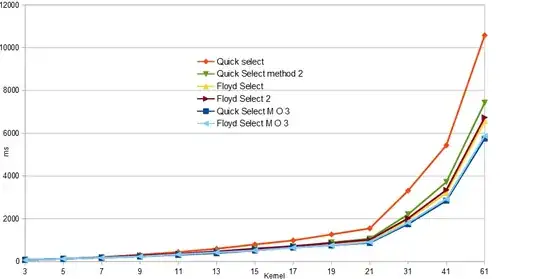
The speed difference is amazing (well at least to me). Here is a chart showing the speeds of the various routines.