The title could be no self-explanatory enough but I need some conceptual help in order to implement a solution to go through an array:
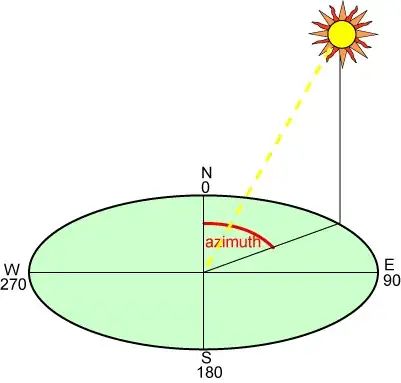
I'm developing a program to calculate the "most shadepath" route between an origin and a destiny, for achieve this an array is fill with all values that represent heights of terrain and each value refers to an UTM coordinate. The sun goes around this array bidimensional and the position of the sun in every moment is determine by the azimut that's simply an angle between the north vector and the perpendicular projection of the star down onto the horizon, in other words, an angle formed between the zenit and the current position of sun in clockwise, with that in mind we now represent an array bidimensional:
If we take four sides like the four cardinal points, the north would be up side, east right side, etc... so the sun rises from the east and set in west not before passing through south.
For a cell value in our array representing our actual location in a geographic position, through azimut, we get the position of sun and between that and our position we need to calculate all cells covering by this projection in order to get posible heights of terrain that block the sun light in that moment and consequently, a shadow is projected.
When sun is in his zenit or 90º, 180º or 270º there's no problem cause cols or rows are the same and no "diagonal" is formed between sun and our position but not occurs when sun is not in his very-east position for example, my question and doubt after all is... How can I determine a way to calculate the increment or decrement for go through col and row cells pointing by the angle of sun and my position for know what diagonal I have to visit cells in order to take heights until the very end of array?
Maybe I'm not being more explicit but I hope you can understand, I could make a graph more explanatory if there are problems of comprehension.
Regards!
Edit with a graphical explanation of what's azimuth is:
Edit
Finally I found a solution for diagonalize using the Xiaolin Wu Algorithm, this algorithm simply creates antialiasing lines between two points, with this in mind, we can make diagonal lines between two array points by their col and row values.
For obtain the border row and col values of the array we can interpolate, if we divide the two dimensional array in four parts intersected by two lines, the vertical line up side represent the azimuth for 0º and 360º and the bottom side 180º, the horizontal line right side will be 90º and 180º for left side; now the four corners of array will be 45º, 135º, 225º and 315º, see above graphics for taking a reference in your mind.
It's like overlaying a circunference in our array for make easy things come to your mind, the more angles values you take as reference for the array the more precise will be the final values when interpolate.
So if we take an example for understanding better what I said before, imagining an array with size of 380x316, if we divide the array in four sides, the middle for cols will be 190 and for rows 158, the 4th quadrant goes from (0,158) for 270º and (190,0) for 0º/360º and 315º would be (0,0) so, using lineal interpolation x2 = ((y2 - y1)(x3 - x1) / (y3 - y1)) + x1 where y coeficients correspond for angle values and x values for predetermined row or cols by angles values so if we take an azimuth of 275º that corresponds with an angle of 4th quadrant we know border value for col in this quadrant is 0 so we have to interpolate for row values, that's it, between 0 and 158, taking between 315º (0,0) and 270º (0,158) our ingonite is the row value between these, so if we replace: x2 = ((275-315)(158-0)/(270-315)) + 0 = 140
Finally the intermediate value between 0 and 158 is 140 or better say [0][140] so if we take any value of our array for example [190][0] passing to drawLine function that takes parameter x origin, y origin, x final and y final we'd obtain all points for make a line between this two points so we can now trace our diagonal line in the array!
Now I paste the algorithm for Xiaolin WU for Java for you will take in mind how is the mechanism, I skipped functions for plotting lines because is not my purpose obviously:
package calculateShadowProjection;
/*
* Xiaolin Wu's line algorithm is an algorithm for line antialiasing, which was presented in the article An Efficient Antialiasing Technique in the July 1991 issue of Computer Graphics, as well as in the article Fast Antialiasing in the June 1992 issue of Dr. Dobb's Journal.
Bresenham's algorithm draws lines extremely quickly, but it does not perform anti-aliasing. In addition, it cannot handle any cases where the line endpoints do not lie exactly on integer points of the pixel grid. A naive approach to anti-aliasing the line would take an extremely long time. Wu's algorithm is comparatively fast, but is still slower than Bresenham's algorithm. The algorithm consists of drawing pairs of pixels straddling the line, each coloured according to its distance from the line. Pixels at the line ends are handled separately. Lines less than one pixel long are handled as a special case.
An extension to the algorithm for circle drawing was presented by Xiaolin Wu in the book Graphics Gems II. Just like the line drawing algorithm is a replacement for Bresenham's line drawing algorithm, the circle drawing algorithm is a replacement for Bresenham's circle drawing algorithm.
*/
public class AlgorithmXiaolinWu {
public AlgorithmXiaolinWu(){
}
public void plot(int x, int y, double c){
}
public int ipart(double x){
return (int)x;
}
public int round(double x){
return ipart(x + 0.5);
}
public double fpart(double x){
if (x<0)
return 1-(x-Math.floor(x));
return x - Math.floor(x);
}
public double rfpart(double x){
return 1 - fpart(x);
}
public void drawLine(double x0, double y0, double x1, double y1){
double aux, x0_orig, x1_orig, y0_orig, y1_orig;
y1_orig=y1;
y0_orig=y0;
x1_orig=x1;
x0_orig=x0;
boolean steep = Math.abs(y1-y0) > Math.abs(x1-x0);
if(steep){
aux = x0;
x0 = y0;
y0 = aux;
aux = x1;
x1 = y1;
y1 = aux;
}
if(x0>x1){
aux = x0;
x0 = x1;
x1 = aux;
aux = y0;
y0 = y1;
y1 = aux;
}
double dx = x1-x0;
double dy = y1-y0;
double gradient = dy / dx;
//handle first endpoint
double xend = round(x0);
double yend = y0 + gradient * (xend - x0);
double xgap = rfpart(x0 + 0.5);
int xpxl1 = (int)(xend); //this will be used in the main loop
int ypxl1 = ipart(yend);
if(steep){
}
else{
}
double intery = yend + gradient; // first y-intersection for the main loop
// handle second endpoint
xend = round(x1);
yend = y1 + gradient * (xend - x1);
xgap = rfpart(x1 + 0.5);
int xpxl2 = (int)(xend); //this will be used in the main loop
int ypxl2 = ipart(yend);
if(steep){
}
else{
}
for(int x = xpxl1+1; x<=xpxl2-1;x++){
if(steep){
System.out.format("Point: [%d][%d]\n", ipart(intery), x);
System.out.format("Point: [%d][%d]\n", ipart(intery)+1, x);
}
else{
System.out.format("Point: [%d][%d]\n", x,ipart(intery));
System.out.format("Point: [%d][%d]\n", x,ipart(intery)+1);
}
intery=intery+gradient;
}
}
public static void main(String[]args){
AlgorithmXiaolinWu axw = new AlgorithmXiaolinWu();
// Test 4º quadrant to 3º quadrant
axw.drawLine(190, 0, 0, 140);
// Test 4º quadrant to 4º quadrant
axw.drawLine(190, 40, 0, 10);
// Test 1º quadrant to 1º quadrant
axw.drawLine(290, 10, 380, 140);
// Test 1º quadrant to 3º quadrant
axw.drawLine(290, 10, 340, 316);
// Test 4º quadrant to 3º quadrant
axw.drawLine(290, 170, 210, 316);
// Test 2º quadrant to 3º quadrant
axw.drawLine(290, 170, 140, 316);
}
}