0

Following my previous question (with great answer from Bart van Ingen Schenau), I noticed a discrepancy I could not wrap my head around:

Bart mentioned that:

The point ON the boundary is by definition the closest you can get. For a closed domain, this point is defined to be the last point inside the domain and for an open domain this point is defined to be the first point that lies outside the domain.

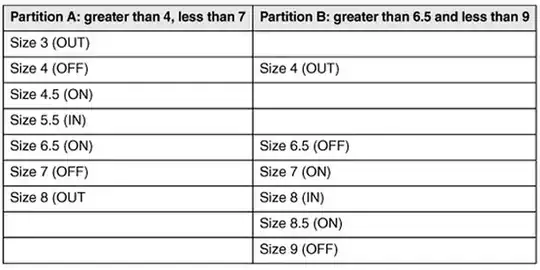
It perfectly works when applying for integers or real numbers but I found a following article in an book. Note the increment is 0.5. enter image description here

But I still do not understand - when Size > 4, they consider 4.5 an ON point but it does not fit the definition - "first point that lies outside the domain." because 4.5 is IMHO in the domain as it is greater than 4. Not sure what is actually the first point outside the domain if 0.5 is the increment.. What is the catch here?

Community
  • 1
user144171
  • 523
  • 5
  • 14
  • Do we know for sure if this is an open or a closed domain? If this is a closed domain the ON values in the chart seem to fit Bart's statement. Is the lack of "or equal to" enough to assume it's open? – Ixrec Mar 05 '15 at 07:55
  • I took an exact snapshot of the page. Above you can see "greater than 7 and less than 7" so I assume it is really an open one. I remind of the fact that there are 0.5 incremets (smallest points). – user144171 Mar 05 '15 at 07:59

0 Answers0