Algorithm or domain for finding cheapest subgraphs that connect vertex pairs

Question

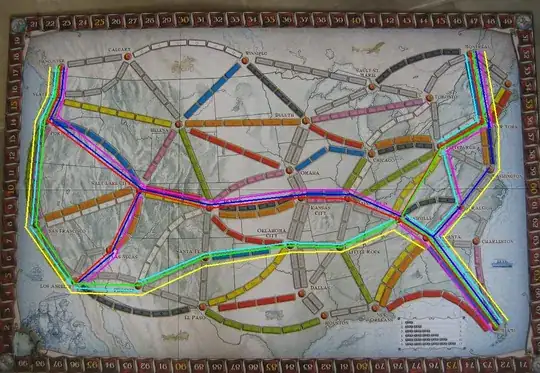
I am currently working on a project inspired by the Ticket to Ride board game. This board game is played on an undirected graph where each vertex represents a city and each edge represents a claimable train line connecting two cities. Players get points by claiming an edge for themselves, scoring points based upon how many cars the route requires to claim. There are also tickets that give bonus points if the player is able to claim a path that connects the two cities. Each player has only 45 cars, so this is a resource allocation problem.

I am trying to write a program that helps agents (humans or AIs) plan which routes to take based upon which tickets that agent needs to complete, which routes the agent has already claimed, and which routes are unavailable due to other players having claimed them. I need an algorithm that finds a set of subgraph(s) such that each ticket has its city in the same subgraph while trying to optimize some criteria (minimum car usage, maximum points per car, etc.). I do not care whether the algorithm gets all the cities in one subgraph, or whether it strings them all out in a line without branching (which would help toward getting the Longest Route bonus); I want something that enables the agent to complete the tickets quickly so he can start working on new ones.

The problem is that I do not have enough familiarity with graph theory to know the name for this type of problem. I have tried searches with text that describes what I am trying to do with no luck. I have also looked in my old textbooks (Introduction to Algorithms and Algorithms in C: Part 5 - Graph Algorithms) to try to find a graph problem domain that seems to relate to my issue; the closest seems to be network flow, but that does not seem to be close enough.

I have tried solving this problem on my own. I wrote an A* that scored each set of subgraphs based upon the estimated minimum distance to a node, but it did not work (as I would have discovered if I had read the Wikipedia article on A* first). I wrote an NSGA-II implementation to try to solve the problem stochastically, but it oddly seems to do worse the closer the initial set of owned edges is to connecting the tickets. In fact, the NSGA-II implementation "freaks out" and finds very strange routes to connect subgraphs when only one route that earlier calls to the algorithm recommended.

Could someone either tell me the name of this domain so I can start doing research, point me to an algorithm, or propose an algorithm that I could try?

Answer 1

It sounds like a combinatorial optimization problem. I would start by reading about branch and bound, and other techniques used in that type of problem. Your representation of a point in the problem space (the current combination) may have an effect on efficiency. If you can create a compact representation, you can compare points, and avoid redundant branch traversals in the tree of combinations. Your cost function is also very important: that is, how good a particular combination (branch) is so far, compared to others.

Answer 2

What you are attempting to do is nontrivial.

You effectively have a graph and are trying to optimize a series of connections based on relatively complicated rules and constraints.

Could someone either tell me the name of this domain so I can start doing research, point me to an algorithm, or propose an algorithm that I could try?

A more formal description of your problem is a constrained optimization problem. There are a variety of methods in literature which deal with such problems, such as combinatorial problems.

Depending on how you have implemented your constraints you can then use a variety of methods. It looks like your constraints are relatively straightforward to list heuristically.

You may find success in modifying your problem to be a traveling salesman problem as there are a lot of methods to deal with these.

I am unfamiliar enough with Ticket to Ride to know how the "points" for a route are calculated. If it is possible to determine a value per edge, this is ideal. You ideally want to convert this into a problem which can be addressed directly with existing methodology. You do NOT want to try to invent your own optimization algorithm to deal with this.

Answer 3

I want to thank those who have posted answers regarding combinatorial optimization. I am going to start studying the field this weekend after I move. In the meantime, I wanted to present my current best effort in case someone else might find it useful.

I have developed a heuristically-driven algorithm that seems to find at least decent results in what may be an acceptable amount of time once I throw part of the processing into an algorithm. I estimate the complexity of the algorithm at O(T! M^T V^2 E^2), where T is the number of pairs to solve (the number of tickets to complete), M is the maximum number of paths of equal length found to connect two vertices using a modified Bellman-Ford, V is the number of vertices in the graph (36 for my map), and E is the number of edges in the graph (78 for my map). For my purposes, M appears to be quite low (probably capped at 6, and frequently lower than that), and I do not expect T to be more than 5 (though 3 is a much more likely ceiling).

The basic assumption behind this algorithm is that the best route will optimally connect one of the pairs of vertices, and the others are more likely to save costs by connecting into this path than to connect directly using their locally optimal paths. The trick is to find the correct order for connecting the pairs that best reduces the cost. The following recursive approach is the backbone for the algorithm:

def planWorker(graph, pairs, ownedEdges, blockedEdges):
    if there are no pairs:
        return 0, empty set
    bestScore, added <- null, empty set
    build a Bellman-Ford table for every vertex in the graph
    // each ownedEdge costs 0
    // each blockedEdge effectively no longer exists in the graph
    for each pair:
        base <- distance to complete pair
        options <- all shortest paths connecting the pair
        // options is a set of sets of edges
        if this is the last ticket:
            bestScore <- base
            for each option:
                path <- option - owned
                added.add(path)
        else:
            for each option:
                subscore, subpaths <- planWorker(graph, pairs - pair, owned + option, blocked)
                total <- base + subscore
                if bestScore == null or total <= bestScore:
                    if bestScore == null or total < bestScore:
                        bestScore <- total
                        added <- empty set
                    for each subpath:
                        added.add(option + subpath)
    return bestScore, added

This algorithm's complexity is O(T! M^T |V|^2 |E|). Called on its own, it finds at least a good threshold against which to compare other paths. I have not yet found an example where it does not find at least a subset of the optimal paths, but I am not assuming that it does find optimal paths because I do not know that my assumption about optimal path structure is correct.

I have found that this algorithm does not find all paths of the same length for a set of pairs. However, by adding an additional search testing untried edges, the algorithm does seem to try them all:

def plan(graph, pairs, owned, blocked):
    bestScore, added <- planWorker(graph, pairs, owned, blocked)
    candidates <- graph.edges - owned - blocked - flatten(added) // the "untried" edges
    for each candidate:
        base = candidate's weight
        score, alternatives <- planWorker(graph, pairs, owned + candidate, blocked)
        total <- base + score
        if total > bestScore:
            continue
        if total < bestScore:
            bestScore = total
            added <- empty set
        for each path in alternatives:
            added <- added + (path + candidate)
    return bestScore, added

The loop multiplies the computational complexity by E, giving the final computational complexity of O(T! M^T V^2 E^2). There's probably additional terms that I am not accounting for that come from the set operations, but my guess is that the sets I am using do not really need more than an additional log E multiple for that.

I have hacked this approach (probably very inefficiently) in Java 8. Running this implementation for four tickets on the Ticket to Ride map with no routes initially owned or blocked takes less than twelve minutes on my unplugged laptop with an Intel Core i7-4710HQ clocked at 2.5 GHz. I can likely speed it up by cutting down on dynamic memory allocation and by threading the candidate checks instead of looping over them synchronously. This algorithm solves the tickets (Los Angeles, Miami), (Los Angeles, New York), (Montreal, Vancouver), and (New York, Seattle) with a cost of 39 cars. The six routes with that length it finds are shown below. The initial planWorker() call finds the green route, and the candidate search finds the other five.