2

I recently stumbled upon a special Sudoku variant and am now struggling to effectively solve it programatically.

Consider the following initial 6x6 grid:
enter image description here

The rules

The red question mark is supposed to represent our secret digit. The secret digit behaves like a normal digit. That is, it has an actual value between 1 and 6, but this value isn't revealed to the player. In this game type, if we create a collision, the newly placed digit would become a neutral element that can be seen as a joker, not colliding with any other digit. For instance, if the secret digit actually was a 6 and we placed a 6 in its row, it would become a neutral element (and we would therewith also know what the secret digit is). We can generate a maximum of one neutral element (meaning that we can only create one collision), a second collision would render the grid unsolved.
Side note: Naturally, this interactive game type doesn't make sense to be printed on a piece of paper; it would e.g. require a client-server infrastructure for the secret not to be revealed to the player.

Analysis

Since the secret digit follows the basic rules, we can deduce that it can't be a 4 in the example grid, but every other digit could be possible. We can also see that there isn't a unique solution; in fact, there usually are hundreds of possible solutions. In a 6x6 initial grid, there is always one secret digit and 6 digits that are pretty randomly placed in the grid (without colliding with each other). This means, the secret could be exposed right off the bet, but we will dismiss the trivial case since it's not fun at all :)

Solving strategy

The most promising strategy would be to find out the secret digit as quickly as possible. That is, we would place digits in its row, column or box until either every possibility is exhausted, or we create a collision. As soon as we know what the secret is, we can solve the puzzle like a normal one (simply ignoring the neutral element if present).

The problem

I want to write an algorithm that finds the secret digit without creating an unsolvable board.
I wrote a rather blunt program which starts by identifying the fields in the secret's row, column and box with the fewest blockers. It then inserts digits in those fields, in an order from fewest blockers to most blockers until the secret can be deduced by collision or exhaustion. In the example grid, it would do something like this:

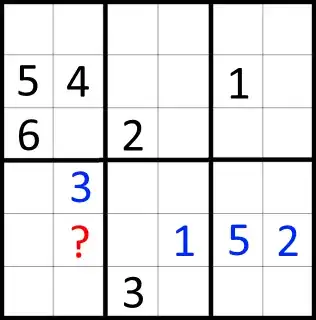
enter image description here
The blue digits would be placed in ascending order (starting with 1). My current alogrithm produces an unsolvable board about 20% of the time, which is unacceptable to me. And that's why I'm asking the question:
What would be a smarter approach, minimizing or even eliminating the possibility of creating an unsolvable puzzle?

P.S.: I appreciate every type of answer; theoretical prose, pseudo-code or real code in a popular language is all fine, I simply want to get the gist of which fields/digits to select for the starting strategy.

Community
  • 1
MCL
  • 129
  • 3
  • It seems you are simply placing the digits onto the board in a manner that does not *immediately* violate any constraints. Also, your algorithm for creating the initial field might be creating unsolvable games. Why don't you modify existing working algorithms to consider your hidden fields? After all, Sudoku is a pretty well-studied game. It seems that in the case of a single hidden field, you'd necessarily end up with the same solution as if that field were free! – amon Dec 28 '14 at 16:24
  • @amon 1) Correct, my starting strategy is currently not much better than just arbitraily putting legal digits around the secret digit. That's what I want to improve. 2) The algorithm for creating the board wasn't supposed to be part of the question and can be assumed to flawlessly create a board with multiple solutions. 3) What working algorithms do you have in mind for this specific Sudoku variant, and especially for carefully finding the secret digit? – MCL Dec 28 '14 at 16:36
  • 4) The secret digit is one specific digit that just isn't initially revealed to the player. That is, it *does* influence the solution, it can't be simply ignored. – MCL Dec 28 '14 at 16:37
  • How is the ? different from an empty field? It also represents a value from 1 to 6 that isn't revealed to the player, and that needs to be found. – Florian F Dec 28 '14 at 21:38
  • @FlorianF You basically explained it yourself. It has a value and behaves like any other digit (can only occur once per row, column and box). The player initially just doesn't know what that value is. He has to find that out by placing digits until either a collision occurs or the all possibilities are exhausted. Imagine it like a computer game where some message pops up if a move collides with the hidden digit. – MCL Dec 28 '14 at 21:43
  • 1
    So you try to put a digit on the same line, and either it works or it says there is a collision, which reveals the value? And you get penalty for creating a collision? – Florian F Dec 28 '14 at 21:50
  • Exactly! If we place a `6` in its row, col or box and produce a collision, we know that the secret digit has to be a `6`. Of course if the secret digit is blocked by 5 other digits, we can deduce its value without any collisions. You don't get penalized exactly. You're allowed to create max. one collision. So the goal is to not to create 2 of them. That is, you don't get extra points if you don't create any collisions, it's just about legally filling the grid with less than 2 collisions. – MCL Dec 28 '14 at 21:52
  • I think the real question is not how to solve it, but how to determine if the solution is solvable given up to N allowed collisions (in this case 1). You do this by assuming that in every guess, the wrong guess is taken. So a given board would only be solvable (w/ n=1) if their was at max one guess between two numbers on a row/column that could have a colision. Any more and it becomes a game of chance. – Lawtonfogle Dec 29 '14 at 18:49
  • @Lawtonfogle Sounds promising. Could you elaborate in an answer? – MCL Dec 29 '14 at 19:40
  • The first rule should be to fill out the obvious. Like row 2. Then in your 2nd drawing, where is your blue 4? You promised to fill in ascending order. Just keep sets for each cell that holds the possible values. And as already said, that question mark is like any blank cell. – ott-- Mar 28 '15 at 22:02

1 Answers1

1

I don't think i understood the WildCard concept to well. Maybe some images of sample configurations on the board would help?

There are already well established Sudoku Solving Algorithms that exist. Some like

Backtracking.

Keep placing numbers one by one until you reach an unsolvable position, then retrace your last step and continue.

Constraint Solving

Each cell has many constraint because of the row, the column and the group of cells. Map out all the constraints of each cell and begin solving the cell where the answer is unique for that contraint. Keep udating the other contraints as numbers are added.

You can find more here

Since there are well established algorithms, one strategy to tackle this problem is to modify the above strategies to include this. Eg: this cell would impose no constraint in its rows, columns and the bigger cell.

I will try to edit with pseudo code for a constraint based solution if I have time.

Community
  • 1
Gaurav Ramanan
  • 624
  • 3
  • 8
  • Solving a normal Sudoku isn't a problem. My question is about which fields to choose in order to find out what the hidden/secret digit is. Imagine an online Sudoku game where you're presented with the example board above. You can place digits anywhere on the free fields of the board. If you place a digit that collides with the secret digit, a neutral element (you could also call it a `0`) will be placed instead. If that makes it clearer, I will incorporate this in my question. – MCL Dec 28 '14 at 17:18
  • The main problem is that you can't calculate a solution before knowing what the secret digit is. Which means, you have to place digits in its row, column or box until you know what digit exactly it is. Only then you can start backtracking for instance. – MCL Dec 28 '14 at 17:22