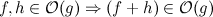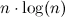I have the follow algorithm which finds duplicates and removes them:
public static int numDuplicatesB(int[] arr) {
Sort.mergesort(arr);
int numDups = 0;
for (int i = 1; i < arr.length; i++) {
if (arr[i] == arr[i - 1]) {
numDups++;
} }
return numDups;
}
I am trying to find the worst case time complexity of this. I know mergesort is nlog(n), and in my for loop I am iterating over the entire data set so that would count as n.
I am unsure what to do with these numbers though. Should I just sum them together? If I were to do that, how would I do it?

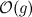 contains all functions that are - starting from some arbitrary large point
contains all functions that are - starting from some arbitrary large point 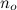 - always smaller than g.
- always smaller than g.