What kind of data cannot be compressed by using the huffman codes and why?
I tried looking for the answer, but I only came across loss-less and lossy compression. I don't really understand what types of data cannot be compressed by huffman and why they can't be compressed using it.
Huffman codes have their basis in the probability that a given character will appear in a sequence. This is why when generating a Huffman prefix tree, the most common characters (those with the highest probability of appearing) are given priority for the shortest prefix.
For example, in the sample text "ABAABACABEDCA" the character 'A' appears 6 times and will be given the shortest Huffman code, 0. 'B' appears 3 times, and will get the next-shortest code, 10, and so on, down to E and D, which both appear only once and will get the longest codes.
In a truly random data set (that is, a string where all possible characters have an equal probability of appearing), then no Huffman tree that can be generated from that string will be any more efficient than any other.
The reason for this is the entropy of the string. A string with high entropy can't be compressed, because more data is required to describe the entropy than would be needed for low-entropy, or highly-structured, data.
The Youtube channel Computerphile has an excellent video that describes this problem quite elegantly.
Lets first look at what compression does. It takes something that is big into something smaller. Yea, thats a really high level way of looking at it, but its an important starting point.
With a lossless compression, there is a point at which you can't squeeze the information any more - its reached its maximum information density.
This gets into the information theory definition of entropy. The pioneer in this field is Claude Shannon who wrote a paper in 1950 titled Prediction and Entropy of Printed English. It turns out that english has between 1.0 to 1.2 bits of information per letter. Think about the word th_ whats that blank? You can predict it - and so there's not much information in that letter.
This really delves into what Huffman encoding does - it squeezes the information as tightly as it can.
What happens if you squeeze more tightly? Well, nothing really. You can't fit more than 1 bit in 1 bit. Once you've compressed the data as optimally as it can be compressed, you can't compress it anymore.
There's a tool out there that will measure how much entropy is in a given stream of bits. I've used it when writing about random numbers. Its ent. The first measure it does is that of the entropy in the stream (it can do other neat tests like calculate pi).
If we take something thats pretty random, like the first 4k bits of pi, we get:
Entropy = 7.954093 bits per byte.
Optimum compression would reduce the size of this 4096 byte file by 0 percent.
Chi square distribution for 4096 samples is 253.00, and randomly would exceed this value 52.36 percent of the times.
Arithmetic mean value of data bytes is 126.6736 (127.5 = random).
Monte Carlo value for Pi is 3.120234604 (error 0.68 percent).
Serial correlation coefficient is 0.028195 (totally uncorrelated = 0.0).
And here we see that you can't compress the digits of pi because there's nearly 8 bits per byte of data there.
So... random numbers, you can't compress those at all.
There are other things that have rather high amounts of information content like encrypted data.
Going back to the simple example of the word th_ and being able to guess what comes next, we know this because of the letter frequencies in English and the valid English words. On the other hand, if we compress this, it is harder to guess what is the next letter and thus there is more information density per letter.
You can see this with (a simple cipher) the Vigenère cipher
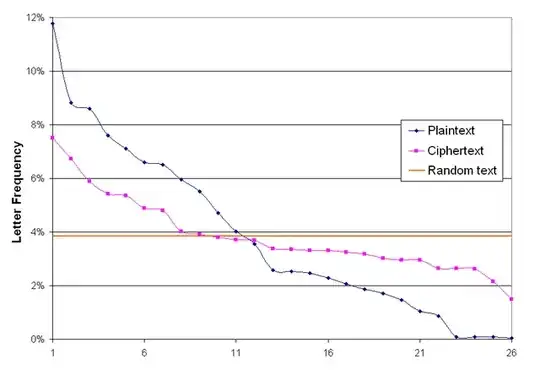
(from Wikipedia: Vigenere letter frequencies)
Here we can see that the letter frequencies are much closer to random than regular English text. This would make it harder for the Huffman encoding to create an optimal encoding for the text.
Modern encryption schemes do an even better job of mixing the information of the key and the pain text together and create a data stream that has extremely high information density, and thus very difficult to predict what character comes next.
And so, those are the things that compression has difficult with and why.
Well compressed data. Note that if the underlying data is highly repetitive you might gain some benefit from compressing the compressed data because the underlying scheme wasn't good enough--compressors are normally built to work fairly fast and that precludes finding an absolutely perfect scheme.
Note, also, that if the "compressed" data isn't really all that compressed you can get a bit this way--I've gotten 2% by zipping a zip--but only when the original zip was full of a whole bunch of small files. The files were being compressed, the file NAMES and other directory info was not.
Encrypted data. A good encryption scheme is basically indistinguishable from random data and thus it's no more compressible than random data is.
