It seems to me like pre-order traversal and DFS are same as in both the cases we traverse from root till the left branch and back to root and then to the right branch recursively. Could any please correct me if I am wrong?
Thanks in advance!
It seems to me like pre-order traversal and DFS are same as in both the cases we traverse from root till the left branch and back to root and then to the right branch recursively. Could any please correct me if I am wrong?
Thanks in advance!
pre order traversal is a traversal, it visits every node in a binary tree
Depth First Search is a search, it goes around an arbitrary graph looking for a certain node (that it works best in a non cyclic graph (a.k.a. tree) is irrelevant)
this alone is a large enough difference to call them difference names
Pre-order traversal and DFS can produce the same result. However, their capabilities are different, in that traversals are only for trees, but DFS is for any graph. All trees are graphs, but not all graphs are trees.
Tree traversal means you visit every node in the tree. Depth-First-Search means you are searching for one specific node in a graph. There are 4 acknowledged tree traversals:
Of these traversals, DFS will produce an identical result to pre-order, when you use DFS as a traversal. The way to do this would be to specify an element that does not exist in the graph, and process all the elements DFS encounters along the way - this would essentially become a traversal.
Here's an excerpt from a notable algorithms textbook
Depth-first search (DFS) is a method for exploring a tree or graph. In a DFS, you go as deep as possible down one path before backing up and trying a different one. DFS algorithm works in a manner similar to preorder traversal of the trees. Like preorder traversal, internally this algorithm also uses stack. - Data Structures and Algorithms Made Easy Java 5ed by Karumanchi N.
Yes, but it should be the opposite way: DFS is similar to PreOrder.
Term PreOrder is more relevant to binary trees and parsers.
It is used to compare with other traversal orders of a binary tree: InOrder, PostOrder and PreOrder.
Topological Sort is similar to Post Order traversal (push the node into stack after visiting all the adjacent nodes).
To traverse a binary tree in Preorder, following operations are carried-out
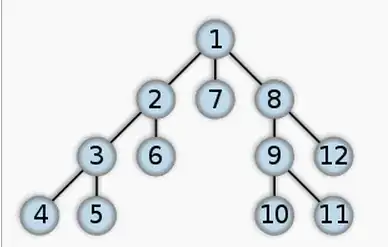
That is in the below image the pre order traversal would be, 1,2,3,6,4,5,7,8,9,10,11,12
In the same image 1,2,3,4,5,6,7,8,9,10,11,12 would be for DFS
DFS Source : http://datastructuresnotes.blogspot.in/2009/02/binary-tree-traversal-preorder-inorder.html
Pre Order Source : Wiki