Maximizing number of nested triangles

Question

There is a finite set of points on a plane (about 1500 points in the current task). I need to construct triangles on those points such as each triangle lies completely inside one larger triangle:

Now I want an algorithm to maximize the number of such triangles. Where can I start?

I think one of the ways would be to choose a "center" and to find three directions from this center with most point density near those directions. Or just choose an arbitrary center triangle manually and then iteratively choose a larger triangle with the least area or the least distance.

Answer 1

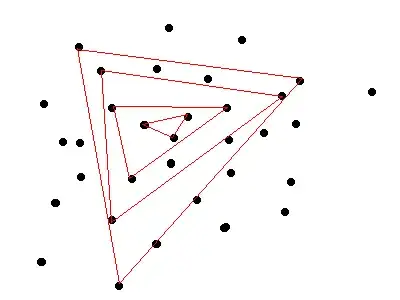
First, create a list of all triangles (subsets of 3 points). Then you make a pairwise comparison of each of two triangles T_i and T_j: either T_i is inside T_j, T_j is inside T_i or none of the two lies inside of the other.

Interpret this as a directed, acyclic graph: the triangles are the vertices of the graph, and each relationship "T_i is inside T_j" defines a directed edge from T_i to T_j. Now finding of a maximum sequence of triangles is just the longest path problem for such kind of graphs. And as you can read in the Wikipedia article, there exist linear time algorithms for solving this problem.

"Linear time" here means "linear to the number of edges" (the number of triangle pairs where one is inside the other). For n points, you have to consider

t := C(n,3)=n*(n-1)*(n-2)/6

triangles (see binomial coefficient), and thus a maximum of

C(t,2) = t*(t-1)/2 

triangle pairs, which can be a huge number with increasing n - its a polynomial of order O(n^6). But since most triangle pairs are not expected to of the type "where one is inside the other", I would expect the real world computational effort to be much smaller. For n below 100 it should be no problem to find a solution directly.

For n >=1.000, this approach most probably won't be fast enough to give you a result in a reasonable amount of time. Thus, better try to solve it with an approximating algorithm like the one suggested by @KonradMorawski, or (easier to implement) simulated annealing. The "simulated annealing" will need a "small modification" step, which may be implemented by removing one or two randomly choosen triangles from your "current solution", and then add triangles again by some kind of "greedy algorithm" with a bit of randomness. You will surely need to experiment with these details to see what works best for your specific problem. As a free resource about this topics, here you find an e-book dealing with different global optimization techniques.

Answer 2

If you are okay with an approximated solution (not necessarily the best one possible), you could try genetic approach.

Find a so-so solution as a starting point - using some simple algorithm such as the one suggested by @Carra - then make, say, a 1000 copies of this initial solution and keep on mutating them randomly. Switching points, trying to add more triangles etc.

Reward the best specimen and throw away poor copies, eg. after each generation you could overwrite the entire gene pool with clones of the best 5%. For best results decrease the temperature with time - it means use aggressive mutation at the beginning, but slower mutation rate towards the end in order to finetune the results once they reach high quality level.

After some iterations you should end up with a fairly good solution.

Answer 3

My gut feeling tells me that this is an NP-complete problem. You can try to find a good solution but not the best one.

So yes, a start would be to pick three points in the middle, start there and create a triangle. Find the closest points to each of these three points and try to create a new rectangle. It should give a decent solution in most cases.

To improve on this, you could run it multiple times with a number of different starting triangles. Or add some randomness to the taking of the closest points. Run it a few times and keep the best solution you've found.