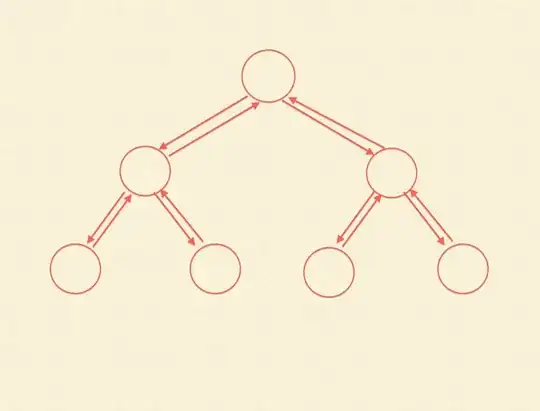
If we make reference to the parent for each node in a tree, do we still have a tree (by definition) anymore?
In computer science, a tree is a widely used abstract data type (ADT) or data structure implementing this ADT that simulates a hierarchical tree structure, with a root value and subtrees of children, represented as a set of linked nodes.