6

I'm working on visualizing a hierarchy. There will be clusters of objects, each cluster containing rectangles of fixed width but variable height. I'd like to arrange these within a rectangular space so as to have equal visual spacing between them, something like this:

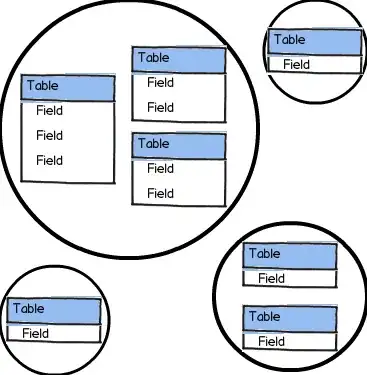
mockup

Before I spend a day inventing the wheel, are there standard algorithms for this kind of distribution and space-filling? If the objects were all the same size, I'd just use a grid.

I'll be using this algorithm at two levels: once to lay out the clusters, and again to lay out the objects within each cluster. The latter would look best if they were arranged within a roughly circular space, but if that complicates things excessively I'm OK with rectangular.

I won't be showing relationships between these objects, so distance minimization is not necessary.

There's a similar question (https://ux.stackexchange.com/questions/29220/what-would-be-the-best-way-to-fill-space-in-an-user-interface-for-irregular-im) about laying out rectangular images while eliminating or minimizing white space. In my case, I want to equalize white space, clusters will be circular, and some clusters will be much larger than others.

Community
  • 1
  • 3
    This is definitely a complex problem. I think you may find some interesting things when you start looking into topics like force-directed graph layout or perhaps some of the other types of layout engines used for GraphViz. They're not a one-for-one match to your problem, but they're in the neighborhood. – J Trana Jan 11 '14 at 06:28
  • There certainly can be an algorithm made to answer this, it actually seems to [me / be] a semi-simple problem. I would say it's akin to adding nodes to a balanced tree; but to make it visually appealing is probably a different problem. – TruthOf42 Jan 27 '14 at 15:45
  • K-means clustering can be used to identify clusters – Dave Hillier Jan 31 '14 at 11:15
  • This is a difficult enough problem when you know the size of your container. It's far more difficult when your container size can stretch if needed. I feel your pain. – Neil Jan 31 '14 at 11:19
  • @JTrana: so far, your comment is the best answer. – kevin cline Jan 31 '14 at 11:51

2 Answers2

1

This is called in mathematics the bin packing problem. There is some example code of the application of the first fit algorithm. Tackling the distribution of white space as required in the second half of your post might be implemented by introducing the concept of elastic "glue" as it is used in the famous typesetting program TeX written by Donald E. Knuth.

Community
  • 1
pefu
  • 193
  • 6
0

I've tackled a similar problem by randomising the positions of each object, then measuring the distance and angle (or normalised gradient) to each other object and nudging them a small amount towards or away from each other based on their relationship to the other object (related=close, unrelated=far), then repeating until the distances start to fall within an acceptable range of what you want. Depending on the size of the data set it can take a while but gives good final results and can look cool in the process! :)

Vorty
  • 1
  • The "random" approach is an acceptable tactic for tackling certain kinds of combinatorial problems. If you are interested, look into complexity theory, including the traveling salesman problem or the bin packing problem. – Jay Elston Feb 12 '14 at 03:09