7

While discussing the development of a network component for our game engine, a member of our team suggested that transmitting either 500 bytes or 1k of data using UDP makes no difference from performance perspective of the system (the time it takes to transmit the data).

He actually said that as long as you don't cross the MTU size, the size of the transmitted data doesn't really matter as it's all the same.

Is that true for UDP? what about TCP?

That sounds just plain wrong to me, but i am not a network expert.

*I've been reading about other companies' game networking architectures, and it seems they're all trying to keep transmitted data to a minimum, making my colleague's claims seem even more unreasonable.

liortal
  • 1,165
  • 3
  • 11
  • 11
  • If you have ever noticed the specifications for an Ethernet switch it is given as BPS (bits/sec) and FPS (frames/sec). These two measurements are mutually exclusive. To attain the BPS spec. the frames have to be max size, and for FPS the frames have to be min size. As long as the data you are transmitting, with overhead, fits into one physical frame, bigger is more efficient. Bear in mind that along the path the data may have to fit in different size physical frames. Basically the statement made to you is correct for both UDP and TCP. – dbasnett Jun 29 '13 at 12:43
  • @dbasnett, I don't think one could say that, *a priori*. Much would depend also on the characteristics of the *data* being transmitted (in real-time transfers you might not even be *able* to fill one physical frame, while when transferring files with FTP, you can), and the *line* they're transmitted over. – LSerni Jun 29 '13 at 13:01
  • The basic statement made by the OP is correct. What protocol, and size of data packets, chosen definitely depends on the application. – dbasnett Jun 29 '13 at 14:17
  • Is your colleague talking about the time it takes for the data to *leave the source*, or to *arrive at the destination*? – Caleth Nov 23 '18 at 13:11

5 Answers5

5

Yes, size matters. Your co-worker's argument is that any amount of traffic up to the MTU will take the same amount of time to transmit, and that simply isn't true.

Forget for a minute that you have any protocols at all, just a pipe where bits go in one end and (hopefully) make out out the other. If the pipe can transfer 8,000 bits per second, 500 bytes (4,000 bits) will take half a second and 1,000 bytes (8,000 bits) will take a full second. This holds true for pretty much every kind of interface because they're all serial. Some interfaces are partially parallel in that they may let you transfer more than one bit per clock cycle, but once you've exceeded that limit, you're serially transferring a stream of whatever those units are. So there's one basic limit right there.

When you add protocols, which are necessary because pipes aren't always reliable or you have lots of pipes that form a network, you add information that tell the protocol implementation what to do with the packet. That information takes up space (and therefore transmission time) that you can no longer use for data and is required overhead, because you can't run the protocol without it.

Your example is a UDP/IP* packet, which contains your payload, an 8-byte header added by the UDP protocol and a 20-byte header added by the IP protocol. If you send 500-byte datagrams, the 28-byte overhead imposed by the protocols will make up 5.3% of the 528-byte packet that has to be sent. Increase the payload to 1,000 bytes and you're sending more of your own data in each 1,028-byte datagram for an overhead rate of 2.7%. If you had a transmission medium that had a large MTU and could swallow a 10,028-byte packet, overhead would shrink even further to 0.3%.

TCP, being a more complex protocol than UDP, has a 20-byte header, which makes the total overhead 40 bytes when run over IP. For your 500- and 1,000-byte payload examples, overhead rates would be 7.4% and 3.8%.

Sending those TCP/IP or UDP/IP packets over Ethernet adds 14 bytes of Ethernet's own header, four bytes of its trailer and 12 bytes of idle time between frames for a total of 30 bytes. As it is with the protocols above, larger payloads mean fewer frames and fewer frames mean less time spent on overhead.

There are a number of reasons why you don't just send arbitrarily-large packets to keep the overhead down. The biggest of those reasons is that you don't want to have to retransmit a whole megabyte of data because you lost six bytes somewhere in the middle. Unless you know your transmission medium is extremely reliable, it's much better to incur the overhead so you only have to re-send a one-kilobyte frame.

The real-world parallel to this would be using 53-foot trucks for shipping. It's a lot cheaper to pack each one as tightly as possible than it is to hire drivers and buy gas for a lot of them to carry just a couple of things each.

*What is commonly called UDP is actually UDP over IP or UDP/IP. UDP can actually be run on top of protocols other than IP, but IP is by far the usual case.

To address dbasnett's comment: The point isn't that UDP is run on top of other protocols, it's that its place in the protocol layer cake means it can be. UDP, being a transport-layer protocol, assumes host addressing has already been taken care of by the network layer. This means you can run UDP (and just UDP, not UDP/IP) across pretty much anything if your only needs were to identify sending and receiving ports. A serial link between two hosts (with no network layer, since addressing would be implicit) would work. Ethernet frames would, too, if MAC addresses were sufficient to identify hosts. I'm not saying anyone actually does this, but a properly-designed network stack will allow replacement of lower layers without the higher ones having to know or care.

Blrfl
  • 20,235
  • 2
  • 49
  • 75
  • I agree that the time the data is on the wire is longer for larger packets. It is also true that UDP has smaller overhead. What other network layer protocol does UDP run on? – dbasnett Jun 29 '13 at 14:07
  • @dbasnett: See the addendum at the end of my post. If the downvote wasn't yours, would the downvoter care to explain how this post could be improved? – Blrfl Jun 29 '13 at 15:30
  • The downvote wasn't mine. UDP as defined in RFC 768 assumes that IP is the underlying protocol. The OSI model was intended to be layered such that any layer could be replaced. – dbasnett Jun 29 '13 at 17:29
  • 1
    @dbasnett: Interestingly, RFC 761, which was written earlier the same year at ISI, and probably also by Jon Postel, goes out of its way not to make the same assumption: `The TCP calls on a lower level protocol module to actually send and receive information over a network. One case is that of the ARPA internetwork system where the lower level module is the Internet Protocol (IP).` There's no technical reason the same can't be done with UDP if you send a zero checksum. – Blrfl Jun 29 '13 at 18:37
  • Actually I've seen some sources say Ethernet is only 14 bytes – information_interchange Nov 23 '18 at 04:54
  • @information_interchange Clarified. The header is 14 bytes, but there's more to it than just that. – Blrfl Nov 23 '18 at 12:39
2

It all depends on what you consider to be the "transmission time". If you take into account the time elapsed between the calls to send() and recv(), this depends on several factors, and packet size might not be so relevant to the calculation. In that case you could, in some (but I repeat, not all!) cases say that whatever you do - TCP, UDP, big or small packets - little changes.

Otherwise, it actually could be beneficial in some scenarios to have smaller packets in order to decrease total transmission time. For example: if you have a high error probability, and you need to retransmit, and you use very large packets, then very soon the error retransmission time begins to dominate the calculation. Increasing packet size will increase the cost and probability of an error, thus increasing the transmission time. In the extreme case of a single packet, the probability of that one packet to be damaged approaches unity, and you may need to retransmit one thousand times. Time increase is now 100000%. With packets one thousand times smaller, ten of them are damaged, you retransmit only those, and overall time is increased by as little as one percent (depending on retransmission protocol).

You also have to consider the overhead. Every packet of B payload bytes you send will have its O bytes of overhead. If we simplify and assume that packet physical transmission time is a linear function of its size (it is not), to transmit N bytes you need to transmit N/B frames, which means (N/B)*(B+O) = N(1 + O/B) bytes, and kN(1+O/B) transmission time. As you can see, the smaller is B, the longer the time. A hypothetical packet of size zero would mean no payload data transmission at all, and therefore infinite time, the exact opposite of the above scenario.

Only at the most abstract level - no overheads and constant-time transmission - yes, transmission time is k(N/B)*B, which is kN and does not depend on B. And, again yes, the first "accident" this model encounters is probably a discontinuity on hitting MTU size.

In general, however, that is not a faithful representation of what really is taking place (think overhead. Think errors. Think lower-layer overheads, plural... and this maybe on a route of several hops), and packet size might matter a lot.

Often, you will have to experiment in order to find the actual best value, because simple heuristics ("the smaller the better", "the bigger the better", etc.) will not yield the best possible result.

A simulated test

I'm here on a XP laptop, so netstat -snap tcp gives me some data to work with re. error rate. I haven't statistics on packet sizes, so I'm assuming they're all around 1500 bytes even if of course they aren't.

I assume that my stats give actual error rate and that a packet is dead if a byte is dead, so that error probability at byte level, Pb, is related to packet error probability Pp by the relation "for a packet to succeed, all bytes must come through intact", i.e.,

1 - Pp = (1 - Pb)^PacketSize

This lets me derive Pb as 1-exp(ln(1 - Pp)/PacketSize). At that point I can recalculate the packet error probability for any other PacketSize, and from that, determine how long it will take to transmit the same payload.

In theory I could claim being right, for it turns out that size matters. But that's nitpicking - I was actually wrong, for in this scenario at least, size matters very very little:

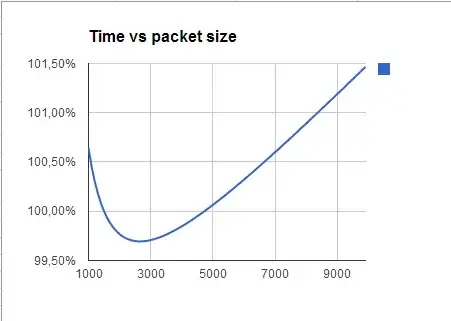
transmit time ratio versus packet size

So, packet size may still influence application design, but certainly not because of data transmission times.

LSerni
  • 2,411
  • 15
  • 21
  • When I started networking (mid 70's) error rates were a huge consideration. Over time it became less of a consideration in most cases. Modern wired / optical networks are almost error free, and wireless networks are getting there. – dbasnett Jun 29 '13 at 14:40
  • My own laptop is far from error-free, but even so, it would appear that you were right. Even a large variation in packet size won't vary total transmission times more than a few fractions of a percent. – LSerni Jun 29 '13 at 16:10
  • 1
    Typically there are three scenarios. One is real-time data (e.g. voice over IP), data transfer (e.g. FTP), and poll/response (e.g. HTTP). In the first two case the size of the packet v. frame rate is of importance. For real-time the size of the packet is smaller but sent at a fairly fixed rate. In data transfer you are more interested in sending as much data as possible. In the case of http data neither much matter. – dbasnett Jun 29 '13 at 17:38
  • I can only upvote your comment. Why don't you add an answer? – LSerni Jun 29 '13 at 19:46
1

Other answers commented on the data size part already but for measuring differences there is another factor relevant:

TCP does not only send the data packages but before sending those it sends extra packages to create a connection, then confirms retrieval of packages and finally sends extra packages to close the connection.

Now the benefit of this is that you get a guarantee that all data was received completely and in the correct order. Building those guarantees in the application is often more complicated than using the proven TCP implementations in the system. Even though Google is currently working on QUIC, an protocol based on UDP to send Web content, I'd suggest using TCP if you need any form of guarantee and UDP only when it is ok that arbitrary packages get lost.

johannes
  • 3,601
  • 2
  • 26
  • 32
1

Blrfl and LSerni answers already address the overhead (in size and then in time) of different packet sizes. They also already address the trade-off about errors.

On the top of that...

An on-line game is highly interactive and even small delays are noticeable, if (and only if) your application is capable of doing something with a smaller chunk (without waiting for the full packet) then you'd better design your protocol to transmit multiple smaller self-contained packets (and to accept the necessary overhead), that's why other companies' gaming networks try to minimize the packet size: the perceived speed is higher if the lag is short.

Let me explain with one example: you need to send the textures of four characters, two cases:

  • You minimize the size of each packet:
    • You send one packet with all required textures but in lo-res.
    • You send four packets, each one for the high-res texture of each character. Application uses immediately that texture to re-render the character.
  • You minimize the number of packets (and then overhead and the raw network performance):
    • You send 1 bigger packet with all high-res textures.

As you can imagine the total time for the second case is relatively WAY lower but the perceived game speed is MUCH worse.

In short: your colleague is wrong (and don't forget that each layout above TCP/UDP will add more and more overhead) but to improve online games performance isn't about raw network speed.

Adriano Repetti
  • 587
  • 4
  • 13
  • Very good point. The discussion did not exist in a vacuum, it directly related to the gaming context. – LSerni Nov 23 '18 at 15:46
0

If you have a custom protocol / a header in each packet --> the smaller you make the packet, the bigger % the header will be!

Lets say the headersize is 100 bytes. And lets say your packet-size options are: either 200 or 400! If you pick 200, your header is 50%, if you pick 400, your header is 25%.

And if you send each packet hundreds/thousands of times, the problem scales!
If you send 10mb / sec, 50% of it will be header data with a packet-size of 200.

So it is better to max out the packet-size, so that the header-size becomes marginal, so that you send more data than meta-data! Really, its all about being efficient. Its common sense!

Edit: And regardless, "UDP" itself is a protocol, that means meta-data is exchanged regardless. So, in fact, it does not matter if you have a header or not, there will always be meta data. So to avoid overhead, maximize package size!

Aphton
  • 98
  • 1
  • 4