Assume I have 4 points (they are 2-dimension), which are different from each other, and I want to know whether they form a square. How to do it? (let the process be as simple as possible.)
-
4I take it you'd need to account for rotated squares? – Martijn Pieters Nov 23 '12 at 12:59
-
Do you have information about the order of the points at all? I.e. can you tell whether two points are adjacent, or form a diagonal? (this info can be used to simplify the process) – Daniel B Nov 23 '12 at 13:53
-
1@DanielB No other information. It just like I have a white paper and draw 4 points on it randomly. Then I want to know whether they form a square. – MarshalSHI Nov 23 '12 at 14:05
-
6Particularly if the points are represented as floating point numbers, it is useful to include a sense of "tolerance" in any of the comparisons suggested below. Exact equality checks can fail for the results of floating point operations, even when we humans would consider them "close enough." – Stephan A. Terre Nov 29 '12 at 22:40
-
This smells like a homework question. Not that there's anything wrong with that. :/ http://whathaveyoutried.com – Jim G. Dec 02 '12 at 23:56
-
@JimG. it is not a homework. -.- – MarshalSHI Dec 03 '12 at 02:00
-
See "Code Golf - Determine if 4 points form a square" at http://codegolf.stackexchange.com/questions/1487/determine-if-4-points-form-a-square/ – Contango Jul 16 '13 at 12:55
12 Answers
Assuming that your square might be rotated against whatever coordinates system you have in place, you can't rely on there being any repetition of X and Y values in your four points.
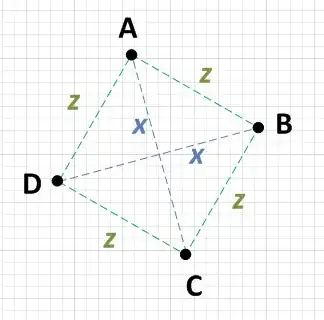
What you can do is calculate the distances between each of the four points. If you find the following to be true, you have a square:
There are two points, say A and C which are distance x from each other, and two other points, say B and D which are also distance x from each other.
Each point {A, B, C, D} is an equal distance from the two points which aren't x away. i.e.: If A is x away from C, then it will be z away from both B and D.
Incidentally, the distance z will have to be SQRT((x^2)/2), but you don't need to confirm this. If conditions 1 and 2 are true then you have a square. NOTE: Some people are concerned about the inefficiency of square root. I didn't say that you should do this calculation, I just said that if you did you would get a predictable result!
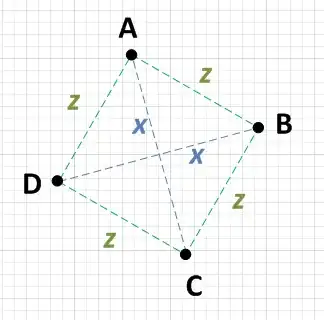
The bare minimum of work that you would need to do would be to pick a point, say A and calculate the distance to each of the other three points. If you can find that A is x from one point and z from two other points, then you just need to check those two other points against each other. If they are also x from each other then you have a square. i.e.:
- AB = z
- AC = x
- AD = z
Since AB = AD, check BD:
- BD = x
Just to be sure, you need to check the other sides: BC and CD.
- BC = z
- CD = z
Since AC = BD and since AB = AD = BC = CD, this is therefore a square.
Along the way, if you find more than two distinct edge distances then the figure cannot be a square, so you can stop looking.
Working Example Implementation
I have created a working example on jsfiddle (see here). In my explanation of the algorithm, I use arbitrary points A, B, C, and D. Those arbitrary points happen to be in a certain order for the sake of walking through the example. The algorithm works even if the points are in a different order, however, the example doesn't necessarily work if those points are in a different order.
Thanks to: meshuai, Blrfl, MSalters and Bart van Ingen Schenau for useful comments to improve this answer.
- 198,589
- 55
- 464
- 673
- 2,388
- 1
- 19
- 17
-
19You can short-circuit this process and not worry about how the points are ordered by measuring the distance between them and keeping track of the number of unique distances you find. Once you exceed two (Joel's _x_ and _z_), the figure isn't a square. – Blrfl Nov 23 '12 at 13:36
-
1the bare min, I don't think it works. At last, you say "it doesn't matter which one, either BC or CD". But if I just check one of them, the figure perhaps is a special Parallelogram. – MarshalSHI Nov 23 '12 at 13:46
-
@Blrfl - Yes, the order is irrelevant. I used ordered points to make the description clearer, but there is nothing in the algorithm that relies on ordering. I think the _shortest circuit_ is five point to point measurements. – Joel Brown Nov 23 '12 at 13:46
-
1
-
If we use the algorithm above the pic, it can help us to get the answer. But we have to calculate all edges. – MarshalSHI Nov 23 '12 at 13:49
-
-
@meshuai - If you like you can check both BC and CD, but once you know AB = AD = BC (plus AC = BD) then there is nowhere else for CD to go. It has to be the same as the other sides. – Joel Brown Nov 23 '12 at 13:52
-
1@Joel Brown . no, if triangle ABC and ABD are Isosceles triangle, which the angle ABC in triangle ABC and angle BAD in triangle ABD are right angle. If C and D are in different side of line AB, that will be a special parallelogram. So, we need check both. – MarshalSHI Nov 23 '12 at 13:59
-
3Another optimisation would be to compare the squared distances, instead of the distances. – vaughandroid Nov 23 '12 at 14:03
-
@meshuai - I've been woodworking long enough to know that if angle ABC = angle BAD and segment AB equals segment CD then ABC = BAD = 90 degrees, but feel free to cross check as much as you like. – Joel Brown Nov 23 '12 at 14:17
-
5@Blrfl: Your test doesn't work. Let ABCD be a diamond with AB=BC=CD=DA=1, AC=1 too (short diagonal), then AD~1.7 (long diagonal)/ You have only two lengths x and z, yet the figure is not a square. – MSalters Nov 23 '12 at 14:23
-
-
2@JoelBrown: It is possible to create a trapezium shape with the diagonals AC = BD = x, the sides AB = BC = AD = z and the last side CD = y != z. – Bart van Ingen Schenau Nov 23 '12 at 14:38
-
@MSalters: If you get to the point where there are more than two unique distances, you can conclusively say the figure isn't a square and bail out early. Whether that optimization is worth doing depends on the expense of doing all of the other math. – Blrfl Nov 23 '12 at 14:40
-
The `SQRT((x^2)/2)` condition needs to be checked in 3+ dimensions. Else you can take a square, raise the corners along one diagonal, and your test passes but it is no longer a square. – btilly Nov 23 '12 at 19:55
-
2
-
You HAVE to check CB and CD, it's not "just to be sure": If you put A, B, D on a square and draw a circle with center A and radius _x_, C could be anywhere on the circle and all the other tests will pass. (Checking _one_ of CB, CD narrows it down to two points, so you need both). – alexis Nov 23 '12 at 23:22
-
This algorithm fails on these 4 points: A=(4,6), B=(5,5), C=(5,6), D=(4,5). It only seems to work if the points are in that particular order, and if you swap B and C around it returns false when it should return true. – Contango Jul 16 '13 at 12:54
-
@Gravitas - You didn't read the algorithm, you just followed the example having redefined the points. Read the algorithm again. Pick a point and test the distance to each other point. Picking A: AC=1, AB=SQRT(2), AD=1. Since AC=AD, and AB != AC, AD -> look at CD, which is=SQRT(2). Since AB=CD, check CB and BD, which both = 1 (= AC, AD) so it's a square. – Joel Brown Jul 16 '13 at 21:55
-
@Joel Brown Yes, the algorithm works perfectly if the points are in that order. However, if I want to check if 4 random points form a square, this algorithm will only work if they are presented in that order. – Contango Jul 18 '13 at 08:04
-
1@Gravitas - Please see my edit, including a link to a jsfiddle that shows that the algorithm works with your points. – Joel Brown Jul 18 '13 at 14:08
-
-
1This fails if the points are duplicated. For example [(1, 1), (2, 2), (1, 1), (2, 2)] is a line segment, not a square. – zzzzBov Jul 27 '16 at 21:26
Pick three of the four points.
Figure out if it's a right isosceles triangle by checking if one of the three vectors between points is equal to another one rotated by 90 degrees.
If so, compute the fourth point by vector addition and compare it to the given fourth point.
Note that this doesn't require expensive square roots, not even multiplication.
- 631
- 4
- 12
-
One of the two good answers. Don't use `sqrt` unless crucial! You don't need to degrade integer calculations to FP... not to mention worsen the precision of the FP computation. – K.Steff Nov 23 '12 at 19:16
-
-
Now that's the right way to do it. Multiplication is indeed not needed here. – COME FROM Nov 29 '12 at 11:06
-
How do you find if 2 vectors are perpendicular to each other without their dot product which involves multiplication? – Pavan Manjunath Apr 02 '18 at 17:48
-
1(x,y) rotated by a right angle is (-y,x) or (y,-x), depending on whether you rotate in the positive or negative direction, respectively. – starblue Apr 03 '18 at 10:12
-
`"...Figure out if it's a right isosceles triangle by checking if one of the three vectors between points is equal to another one rotated by 90 degrees..."` Could you please tell how can I do this? – Suhail Gupta Aug 19 '19 at 07:40
-
1A vector (x,y) rotated left by a right angle is (-y,x), and rotated right (y,-x). – starblue Aug 19 '19 at 19:20
I think the easiest solution is the following:
First, calculate the center of the 4 points:
center = (A + B + C + D)/4Then calculate the vector
A - center. Let this bev := (x,y)Let
v2be the vectorvrotated by 90 degrees:v2 := (-y, x)Now the other points should be
center - v,center + v2andcenter - v2.
The advantage of this solution is that you don't have to use square roots at all.
- 531
- 3
- 8
-
2Yeah. This is the most comprehensible and probably the easiest to implement as well. – Eric G Nov 30 '12 at 17:39
-
It seems like vector equality of segments. Can anyone please elaborate or prove why it works? – vCillusion Jul 18 '16 at 16:16
-
It fails specifically for case (0,0), (2,1), (3,-1), (1, -2) -- square not aligned to axis – vCillusion Jul 18 '16 at 16:52
-
1It works for this case. The center point is (1.5, -0.5), first point is (0, 0) and three other points are (1.5, -0.5)+(1.5, -0.5) = (3, -1); (1.5, -0.5)+(0.5, 1.5) = (2, 1) and (1.5, -0.5)-(0.5, 1.5) = (1, -2) which means it's a square. The proof is .. symmetry? – aragaer Jul 27 '16 at 22:36
-
1The "distance solution" needs square roots, but there's the "squared distance solution", which needs none. Yours may be still more efficient... – maaartinus Nov 18 '19 at 21:44
-
this is a pretty nice way because one doesn't have to care about the order of points. Also fast. – Sopel Nov 19 '19 at 22:43
I'm sorry but some answers don't apply.
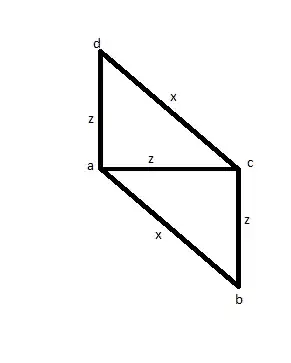
For the case you measure 3 edges (let's say AB, AC and AD) to find that two have the same size (let's say AC and AD) and one is bigger (let's say AB). Then you would measure CD to see if it's the same size of AB, and you find that it is. Instead of a square, you could have the picture below, and that makes it a wrong solution.
Then you try some other solution: measure all the distances at least once: AB, AC, AD, BC, BD, CD. Then you find that 4 of then are equal, and the other 2 are also equal among themselves. But you could just have a picture like below:
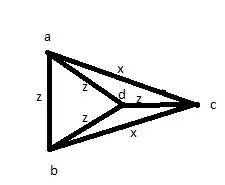
So, those answers aren't correct, despite the high upvotes they received.
One possible solution: if the two equal measures don't connect the same point. So: if AB and CD are the same lenght, all the other combinations (AC, AD, BC, BD) are also equal, you have a square. If you have the same point making the biggest length (AB and AC is the biggest, and all the others are equal), you have one of the pictures above.
- 223
- 3
- 9
-
no, his algorithm said the 2 edges of distances x do not share a point. but you just share C. So, assume A-C is x, then B-D should be another x instead of your B-C. – MarshalSHI Nov 23 '12 at 15:15
Let the four points have coordinate vectors a, b, c, d.
Then lets call their differences w=(a-d), x=(b-a), y=(c-b), z=(d-c).
Then w is orthogonal to a if you can create w from a by a 90-degree-rotation. Mathematically the 90-degree-rotation-matrix in 2-space is ( ( 0, -1 ), ( 1, 0 ) ). Thus, the condition whether w is a 90-degree-rotated a results in
( w_1 == -x_2 and w_2 == x_1 )
If this holds, then you need to check that w == -y and x == -z, or
( ( w_1 == -y_1 and w_2 == -y_2 ) and ( x_1 == -z_1 and x_2 == -z_2 ) )
If those three relations hold, a, b, c, d make an oriented square.
- 31
- 1
-
1
-
No, the first conditionis not met by orthogonal, but not equally lengthed vectors. – Mark Salzer Nov 23 '12 at 15:44
-
1yeah, I just miss the first one. But the 4 points are not ordered. So, we need more steps, I think, in order to confirm. – MarshalSHI Nov 23 '12 at 15:58
-
Yes... if no cleverer idea arises, one whould need to loop. I think one needs an outer loop to calculate w, x, y, z from each possible ordering of a, b, c, d, and one inner loop for each possible ordering of the w, x, y, z tuple. – Mark Salzer Nov 23 '12 at 17:08
Similar to the answer by starblue
Pick any three of the four points.
Look for a right angled vertex among them: By checking if the dot product of any two of the three vectors is zero. If not found, not a square.
Check whether the vertices adjacent to this angle are right angled too. If not, not a square.
Check whether diagonals are perpendicular: If the dot product of the vectors between the first and fourth vertex and the other two vertices (diagonals) is zero, then its a square.
- 131
- 4
-
Good idea, but you still need to check that the 4th vertex is at the right distance from the other points. You only check that it is on the diagonal. – starblue Dec 01 '12 at 15:49
-
I think you can do this with simple addition and subtraction and finding min/max. Terms (matches other people's diagram):
- Point with highest y value => A
- highest x => B
- lowest y => C
- lowest x => D
If 4 points share only 2 x values and 2 y values you have a level square.
Otherwise, you have a square if your points satisfy the following:
- A.x + C.x = B.x + D.x
- A.y + C.y = B.y + D.y
- A.y - C.y = B.x - D.x
Explanation: The line segments A-C and B-D should meet at their midpoints. Thus (A.x + C.x) / 2 is the midpoint of A-C and (B.x + D.x) / 2 is the midpoint of B-D. Multiply each side of this equation by 2 to get my first equation. The second equation is the same thing for Y-values. Diamond-shapes (rhomboids) will satisfy these properties, so you need to check that you have equal sides - that the width is the same as the height. That's the third equation.
- 14,890
- 6
- 47
- 75
There are some good answers here, but the question asked for the simplest approach. I gave this some quick thought and this is how I would do it.
You can tell if four points represent a square (even if rotated), but finding the average of the four points.
R = (A+B+C+D)/4
Once you have the average, the distance between each point and the average would have to be the same for all four points.
if(dist(R,A) == dist(R,B) == dist(R,C) == dist(R,D) then
print "Is Square"
else
print "Is Not Square"
EDIT:
My mistake. That would only tell you if the form points were on a circle. If you also check the distance between points, then it must be a square.
if(dist(R,A) == dist(R,B) == dist(R,C) == dist(R,D) AND
(dist(A,B) == dist(B,C) == dist(C,D) == dist(A,D) then
print "Is Square"
else
print "Is Not Square"
This assumes that points A,B,C,D do not cross (as in have a valid winding order).
- 13,040
- 4
- 48
- 81
this is not an answer according to the standards set, but I hope this helps:
[Copied from the link below so you don't have to open the link] Python 76 characters
def S(A):c=sum(A)/4.0;return set(A)==set((A[0]-c)*1j**i+c for i in range(4))
Function S takes a list of complex numbers as its input (A). If we know both the centre and one corner of a square, we can reconstruct the square by rotating the corner 90,180 and 270 degrees around the centre point (c). On the complex plane rotation by 90 degrees about the origin is done by multiplying the point by i. If our original shape and the reconstructed square have the same points then it must have been a square.
This was taken from : Determine if 4 points form a square
If you like the answer, I say, take some moments out to thank the person, or up-vote his answer on that page.
- 153
- 6
-
1You could summarize the algorithm here. You are linking to another SE site, which is slightly better than pointing to another site, but we want the answer to be on *this* page, where the question is being asked. Now people have to click again to learn what the answer might be. – Martijn Pieters Nov 29 '12 at 15:01
Basic idea (this answers the question of whether I was contributing something new, which was asked by the bot when I clicked to provide an answer):
- a rhombus with equal diagonals is a square.
- "simple as possible" includes:
- no division,
- no square roots,
- no branching,
- no searching,
- no angle-checking or -chasing,
- no vectors,
- no transformations,
- no complex numbers,
- no multiline functions, and
- no importing of special packages (use built-in stuff only).
- (And no Imperial entantglements!)
My solution in R is presented below. I am assuming that there are exactly four points and that, per the problem statement, it has already been determined that the points are unique.
sumsq <- function(x) sum(x^2)
quadrances.xy <- function(xy) vapply(
as.data.frame(t(diff(xy)), optional=T), sumsq, 1)
See the works of Norman Wildberger, especially his YouTube videos (Real fish, real numbers, real jobs et seq.) and his book Divine Proportions for a discussion of "quadrance."
xy refers to a kind of matrix accepted by R's plot, points, and lines functions.
Application of as.data.frame is a trick to get R to do things column-wise.
The optional=T clause eliminates names, which are not used, anyway.
quadrances.xy..i2. <- function(xy, i2) vapply(
as.data.frame(i2, optional=T),
function(k) quadrances.xy(m[k,]),
1)
This is a function to compute the quadrances between the specified points, where pairs of points are specified by the i2 argument. The i2 symbol refers to an index matrix which has one column per index, and 2 elements per column (the same kind of matrix returned by the combn function).
quadrance.every.xy <- function(xy, .which=combn(nrow(xy), 2))
quadrances.xy..i2.(xy, .which)
The .which is presented as an argument merely to expose it to formals and to attempt to communicate what is going on.
is.square.xy <- function(xy) {
qq <- sort(quadrance.every.xy(xy))
all(qq[2:4] == qq[1]) && # ALL SIDES (SHORT QUADRANCES) EQUAL
qq[5] == qq[6] # ALL DIAGONALS (LONG QUADRANCES) EQUAL
}
I said "simple" included no multiline functions. You'll have to excuse this two-line function.
xy <- t(matrix(c(3,0, 7,3, 4,7, 0,4), ncol=4))
xy
# [,1] [,2]
# [1,] 3 0
# [2,] 7 3
# [3,] 4 7
# [4,] 0 4
is.square.xy(xy)
# [1] TRUE
Note that the first four functions are useful in their own right, apart from the question about the four points.
- 121
- 3
Assume four points A = (ax, ay), B = (bx, by), C = (cx, cy), D = (dx, dy), and they form the points of a square in anti-clockwise ordering. We move the points so that A is at (0, 0) by subtracting ax from bx, cx, and dx, and subtracting ay from by, cy, and dy, setting ax = ay = 0.
If the points are exactly the corners of a square in anti-clockwise ordering, then given A and B, we can calculate where C and D are: We should have (cx, cy) = (bx - by, bx + by) and (dx, dy) = (-by, bx). So we calculate the squared distance from where C and D are, to where they should be: errC = (cx - bx + by)^2 + (cy - bx - by)^2, and errD = (dx + by)^2 + (dy - bx)^2. We add these, and divide by (bx^2 + by^2), giving err = (errC + errD) / (bx^2 + by^2).
The result err would be 0 if a perfect square, or a small number if almost a square, and the number would stay unchanged except for rounding errors if we translate, scale, or rotate the points of the square. So we can use err to decide how good a square we have.
But we don't know the ordering of the points. B and D should be at the same distance from A; if we multiply this by the square root of 2, that should be the distance from A to C. We use this to figure out which point is C: Calculate distB = bx^2 + by^2, distD = dx^2 + dy^2. If distD ≥ 1.5 distB, then we swap C and D; if distB ≥ 1.5 distD then we swap C and B. Now C is right.
We can also figure out which points are B and D: If we guessed wrong which one is B and which one is D, then our calculation puts D into the completely wrong place, exactly opposite from where it is. So if errD ≥ (bx^2 + by^2), then we swap B and D.
This will arrange B, C and D correctly if we have a square indeed or at least roughly a square. But if we don’t have even roughly a square, we know the error calculation at the end will show this.
Summary:
- Subtract ax from bx, cx, dx. Subtract ay from by, cy, dy.
- Let distB = bx^2 + by^2, distD = dx^2 + dy^2.
- If distD ≥ 1.5 * distB, swap C and D and calculate distD again.
- Otherwise, if distB ≥ 1.5 * distD, swap B and C and calculate distB again.
- Let errD = (dx + by)^2 + (dy - bx)^2.
- If errD ≥ distB then swap B and D, swap distB and distD, calculate errD again.
- Let errC = (cx - bx + by)^2 + (cy - bx - by)^2.
- Let err = (errC + errD) / distB.
- Decide whether we have a square or almost a square depending on the value of err.
If we know the order of the points, this can obviously be simplified.
- 42,090
- 4
- 59
- 119
Solution is similar to thinking media.
First step:
x = (A+B+C+D)/4
f=0
if(dist(x,A) == dist(x,B) == dist(x,C) == dist(x,D)
f=1
else
f=0
This property is followed by square because it is cyclic. now a circle to follow this property. so, now just check
if(A.B==B.C==C.D==D.A==0)
f=1
else
f=0
if (f==1)
square
else
not square
Here A.B means dot product of A and B
- 1,140
- 4
- 16
- 22
- 11