The Big Oh notation (O, Theta, Omega) is about growth rates of functions.
When you implement an algorithm, it has a certain characteristic how the runtime changes when you increase the dataset operates on. Now, you may optimize the algorithm so it runs faster by a factor of 100. Sure, this is great, but essentially, it's still the same algorithm. Similarly, in a few years, computers may be twice as fast as they are today.
The Landau notation abstracts away these constant factors. It doesn't care about whether an algorithm f is always twice as fast as another algorithm g: Maybe g can be optimized to run 4 times faster, or you might be able to buy faster hardware instead. If you look at it from this perspective, you might say they are "the same". (That is not to say you can (always) ignore constant factors in practice.)
Big oh specifies an upper bound, it's similar to the <= relation.
You will agree that 1 < 2 is true. Does that mean that 1 cannot be less than any other number? Certainly not. There is an infinite amount of numbers that are bigger than 1.
With growth rates, it's similar. O(n) denotes the set of all functions, that grow linearly (or more slowly). O(n^2) on the other hand denotes all those functions, that grow with quadratic compelxity (or slower). I am sure that you will agree that a linear function grows more slowly than a quadratic function.
This is why a function can be in more than one "Big-oh" class.
Here is a comparison of different functions with  : (from Knuth's Concrete mathematics)
: (from Knuth's Concrete mathematics)
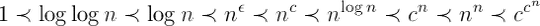
From left to right, functions grow faster.
Also, 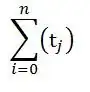 , meaning n^2 grows faster than n^1 because 2 > 1.
, meaning n^2 grows faster than n^1 because 2 > 1.
Definitions
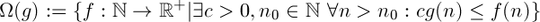
"f grows faster or equally fast as g"
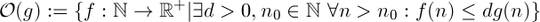
"f grows slower or equally fast as g"
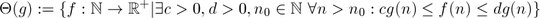
The combination of the above two. It says the function f grows "equally fast" as g. It's an equivalence relation.
Interpretation
Let's say you have two algorithms, f and g.
Omega
Assuming 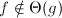 ,
, 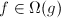 means that no matter your budget, there is no constant amount of computing power that you can add to your system, such that
means that no matter your budget, there is no constant amount of computing power that you can add to your system, such that f will always run as fast as g.
Big oh
Assuming 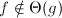 ,
, 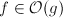 means that if you have enough data,
means that if you have enough data, f will always run faster than g, no matter how much computing power you add to your system.
Proof
If you are really trying to prove this, you need to show using the definitions of the Landau notation that your function satisfies the necessary conditions.
So you need to find values for c, d, n_0 such that the condition holds.
Here is how you can do that for the lower bound with c:

It is important to realize, that me arbitrarily defining c as being smaller than a-1 is perfectly fine. The definition of Theta(g) says that "there exists a c". It can be any value as long as it is bigger than 0. (If a is a positive real number, you would need to change the proof slightly however, because a - 1 might actually be negative)
(I am assuming a to be positive, otherwise the function will always be negative for big values of n, which makes no sense for a function denoting the runtime.)
You can try doing it for the upper bound, it's quite similar. If you don't know how, I can provide a proof for you.
Hint: start with d > a + 1
Attention
It is important that you do not prove it the wrong way around. If you assume that (an + b) is in O(n) and go from there, you have not proven what you wanted. You will need to verify that all of your steps go both way, i.e. instead of => you have <=>.
 : (from Knuth's Concrete mathematics)
: (from Knuth's Concrete mathematics)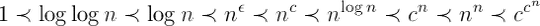
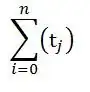 , meaning n^2 grows faster than n^1 because 2 > 1.
, meaning n^2 grows faster than n^1 because 2 > 1.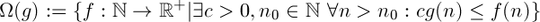
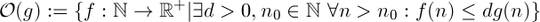
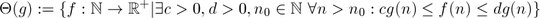
 ,
,  means that no matter your budget, there is no constant amount of computing power that you can add to your system, such that
means that no matter your budget, there is no constant amount of computing power that you can add to your system, such that 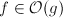 means that if you have enough data,
means that if you have enough data, 