Let's say we're going from 1 to 5. The shortest route will be 1-4-3-5 (total: 60 km).
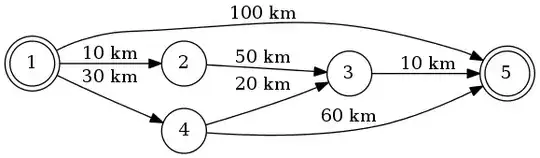
We can use Dijkstra's algorithm to do that.
Now the problem is, the shortest route is not always the fastest one, because of traffic jams or other factors.
For example:
- 1-2 is known to have frequent traffic jams, so it should be avoided.
- Suddenly a car accident happens along 4-3, so it should be avoided too.
- Etc...
So probably we can speed on the route 1-4-5, because of no traffic jams/accidents, so will arrive at 5 faster.
Well that's the general idea, and I haven't think about more details yet.
Is there any algorithm to solve this problem?