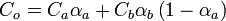The perfect crossfade

Question

I find it hard to describe this problem in words, which is why I made a video (45 seconds) to illustrate it. Here's a preview of the questions, please have a look at it on Vimeo: http://vimeo.com/epologee/perfect-crossfade

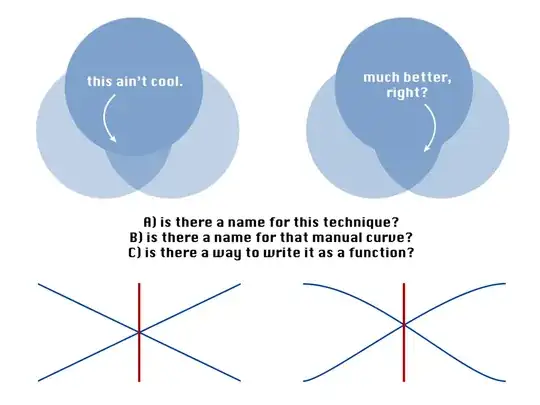
The issue of creating a flawless crossfade or dissolve of two images or shapes has been recurring to me in a number of fields over the last decade. First in video editing, then in Flash animation and now in iOS programming. When you start googling it, there are many workarounds to be found, but I really want to solve this without a hack this time.

The summary:
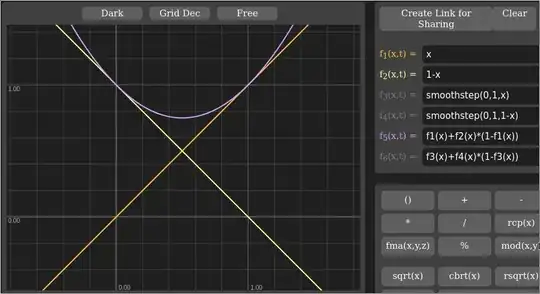
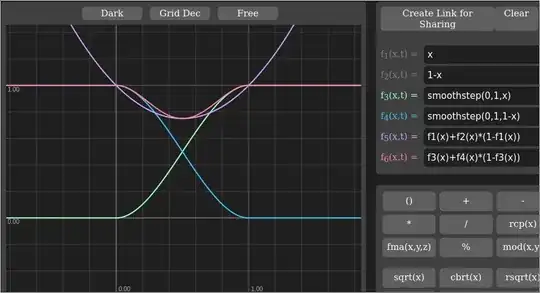
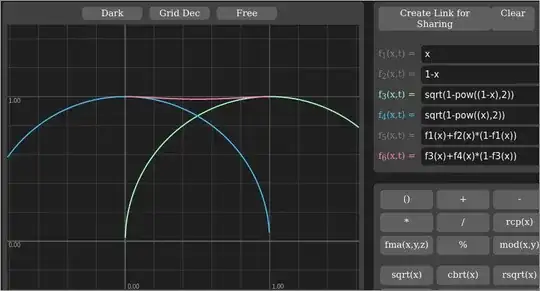
What is the name of the technique or curve to apply in crossfading two semi-transparent, same-colored bitmaps, if you want the resulting transparency to match the original of either one?

Is there a (mathematical) function to calculate the neccessary partial transparency/alpha values during the fade?

Are there programming languages that have these functions as a preset, similar to the ease in, ease out or ease in out functions found in ActionScript or Cocoa?

Update: In addition to the video, I've made a sample project (requires Xcode and iOS SDK) and posted it on github. It shows the same animation as the video but this time with squares: https://github.com/epologee/StackOverflow-Example-Code

Answer 1

I am afraid that's not possible. This is how transparency is calculated when two objects overlay: http://en.wikipedia.org/wiki/Alpha_compositing

One of the objects must have an opacity of 1 if you don't want the overlay area to be seen through.

Answer 2

I don't know what the name might be in the realm of video editing, but I'd call the curve an S-curve or sigmoid curve. It should be very simple to produce the cross-fade you're looking for in iOS using Core Animation's kCAMediaTimingFunctionEaseInEaseOut timing function. Just animate the alpha property of two views in opposite directions (one 0->1, one 1->0) using that timing function:

[UIView beginAnimations:@"crossfade" context:nil];
[UIView setAnimationDuration:1.0];
[UIView setAnimationCurve:UIViewAnimationCurveEaseInOut];
view1.alpha = 0.0;
view2.alpha = 1.0;
[UIView commitAnimations];

Note: You should really use the blocks-based animation methods instead of UIView's convenience methods. I used UIView's methods above because it's very easy to understand, and easy to type from memory. Using blocks isn't much more difficult, though.

Addendum: If you don't like UIViewAnimationEaseInOut, you can create your own timing function as described in Timing, Timespaces, and CAAnimation. That's a bit more advanced than the simple animation illustrated above, but it gives you all the control you want.

Answer 3

In computer graphics, this kind of function is called smoothstep. When used to crossfade, it determines the global alpha value for the composition.

If the input images have an alpha channel, you should first make sure that the alpha is premultiplied. Then, you can do the crossfade composition straightforwardly, using the smoothstep alpha on each channel [X = A*alpha + B*(1-alpha)], and expect reasonable results.

Answer 4

While it's true that the perfect result cannot be achieved, it is also true that, as you have discovered, the problems can be mitigated somewhat.

And we can do something more formal than "some manual curve" (though that's fine in many cases, too).

The crux of the problem with the plain linear version is that at the midpoint, where you have each object half transparent, the full transparency dips low. Even using an unmodified smoothstep does not fix this, since it also has a crossing point at 0.5. This is made more clear with some graphs:

You can see a live version here, but here are some screenshots:

In these graphs, f5(x) and f6(x) are the final output alpha values, which we'd like to stay "1" across the fade.

Plain linear crossfade:

Plain smoothstep, with the linear version left for comparison:

As you can see, in both cases there is a "dip" in the value in the middle. In your "fixed" version from the question, the actual reason it works better is that the crossing point is above 0.5 - not due to the curves being smooth.

Here is a version using a circular easing function, so the crossing point is quite high:

As you can see, the dip is much less exaggerated, since the two "parent" easing curves cross at a much higher point.

What easing curves you want to use is up to you, of course, but hopefully this discussion helps ground those investigations.

---

Aside: I want to point out that there actually is a perfect solution, but unfortunately it is the step function — that is, just blinking from one to the other, without a smooth dissolve. Probably not very helpful, but it became apparent from fiddling with easing curves that it does in fact fit the bill (:

Answer 5

You can use the exponential decay function:

Alpha1(time) = 1 - exp(-time / (0.2 * transitionTime)); // fade in
Alpha2(time) = 1 - Alpha1(time); // fade out

Your graph looks more like:

Alpha1(time) = sin(time * 0.5 * pi / transitionTime); // fade in
Alpha2(time) = cos(time * 0.5 * pi / transitionTime); // fade out