68

I am aware that floating point arithmetic has precision problems. I usually overcome them by switching to a fixed decimal representation of the number, or simply by neglecting the error.

However, I do not know what are the causes of this inaccuracy. Why are there so many rounding issues with float numbers?

nmat
  • 813
  • 1
  • 7
  • 6
  • 29
    To be precise, it's not really the *error* caused by rounding that most people worry about -- it's the fact that binary floating-point rounding behaves in unintuitive ways. Switching to a decimal representation can make the rounding behave in a more intuitive way, but in exchange you will nearly always *increase* the relative error (or else have to increase the storage space to compensate). – Daniel Pryden Aug 15 '11 at 16:35
  • 14
    My attempt to clear up the most common confusions: http://floating-point-gui.de/ – Michael Borgwardt Aug 16 '11 at 11:22
  • i think what @DanielPryden means is *"Switching to a [fixed-point] representation can make the rounding behave in a more intuitive way..."*. what *causes* rounding problems, whether it's fixed or floating-point numbers is the finite word width of either. it's just that, with floating-point, the magnitude of the rounding error normally remains roughly proportional to the magnitude of the number being rounded. (except when you get really small and to "denormalized" numbers.) – robert bristow-johnson Mar 27 '15 at 04:56
  • @robert: That's not exactly what I was referring to. The "error" most people encounter with floating point isn't anything to do with floating point per se, it's the base. IEEE-754 floats and doubles use an exponent in base 2, which means that fractional numbers round off to negative powers of two (1/2, 1/16, 1/1024, etc.) rather than negative powers of 10 (1/10, 1/1000, etc.) This leads to unintuitive results like 0.1 rounding to 0.1000001 and similar issues. – Daniel Pryden Mar 27 '15 at 06:02
  • You can do floating point numbers in base 10 -- that's how .NET's `decimal` type works. Fixed point, on the other hand, is different. As long as your range is limited, fixed point is a fine answer. But the restrictive range makes fixed point unsuitable for many mathematical applications, and implementations of fixed point numbers are often not well optimized in hardware as a result. – Daniel Pryden Mar 27 '15 at 06:06
  • i see @DanielPryden. so the precision problems that you're referring to are more about how floating point numbers are *displayed* as base-10 that we human beings read. inside the computer, the "rounding issues" don't really know or care about what base we display the numbers as. but you're right, 0.1 cannot be precisely represented as an IEEE-754 float or double (but you can get awful close). – robert bristow-johnson Mar 27 '15 at 06:09
  • *"You can do floating point numbers in base 10 ..."* oooh, weird! like BCD (binary-coded decimal)??? ick. – robert bristow-johnson Mar 27 '15 at 06:10
  • *"the restrictive range makes fixed point unsuitable for many mathematical applications, ..."* well, my answer below (describing a moving average operation) describes a mathematical operation where fixed-point exceeds floating-point for "suitability" ... *"and implementations of fixed point numbers are often not well optimized in hardware as a result."* well, the hardware likely just does 2's complement integer and maybe has an FPU. anyway, doing fixed-point using integer variables is a matter of noting the 2^p scaling and dealing with it with the left or right shift operators. – robert bristow-johnson Mar 27 '15 at 06:15
  • @robert: The point I was trying to make was that the OP's premise for this question is not necessarily valid. Floating point math doesn't introduce more error than fixed point -- actually it can introduce *less error* (especially relative to bits used). There are good reasons to use fixed point or decimal floating point, but "not understanding how binary floating point behaves" isn't a good reason IMO. And BTW, no, .NET's `decimal` isn't like BCD at all -- it has a mantissa and exponent, just in base 10. BCD is a whole other kettle of fish. :-) – Daniel Pryden Mar 27 '15 at 06:15
  • *"Floating point math doesn't introduce more error than fixed point ..."* it **can**!! the moving-average filter (implemented using recursion) is an example of where floating-point will introduce more error than fixed. that is because what gets subtracted might not be exactly what was added before. but with fixed point, you can make sure that **exactly** what was added earlier is subtracted now. but most of the time, floating point has less rounding error problems than fixed. – robert bristow-johnson Mar 27 '15 at 06:21
  • BTW, all's i mean for BCD is that each base-10 digit is isolated as a 4-bit number that never exceeds `0b0000000000001001` (which is 9). perhaps the exponent can be binary (since it's always an integer), but the mantissa would be an array of `unsigned int` or `unsigned short` with value never exceeding 9. – robert bristow-johnson Mar 27 '15 at 06:25
  • I don't know if this is a rounding error or not but `141700000000000000000000000000000.00 - 273.15` returns `141700000000000000000000000000000.00` instead of `141699999999999999999999999999737.85`, this seems to be a rather large difference in value to simply be a rounding error, is there some other issue with floats that is causing this? – RWolfe Jan 25 '22 at 00:54

7 Answers7

89

This is because some fractions need a very large (or even infinite) amount of places to be expressed without rounding. This holds true for decimal notation as much as for binary or any other. If you would limit the amount of decimal places to use for your calculations (and avoid making calculations in fraction notation), you would have to round even a simple expression as 1/3 + 1/3. Instead of writing 2/3 as a result you would have to write 0.33333 + 0.33333 = 0.66666 which is not identical to 2/3.

In case of a computer the number of digits is limited by the technical nature of its memory and CPU registers. The binary notation used internally adds some more difficulties. Computers normally can't express numbers in fraction notation, though some programming languages add this ability, which allows those problems to be avoided to a certain degree.

What Every Computer Scientist Should Know About Floating-Point Arithmetic

Spooky
  • 103
  • 5
thorsten müller
  • 12,058
  • 4
  • 49
  • 54
  • 13
    Spot on. But I would also note that some numbers that terminate in decimal don't terminate in binary. In particular 0.1 is a recurring number in binary and so no floating point binary number can exactly represent 0.1. – Jack Aidley Mar 04 '13 at 13:39
  • 4
    Floating points aren't just useful for a lot of decimal places. 32 bit integers can only count up to about 4 billion, but a 32 bit float can be almost infinitely large. – Abhi Beckert Jan 27 '15 at 05:35
  • 8
    In particular, the fractions we can express as finite decimals are those whose denominators' prime factorization contains only 2 and 5 (e.g. we can express 3/10 and 7/25, but not 11/18). When we move to binary, we lose the factor of 5, so that only the dyadic rationals (e.g. 1/4, 3/128) can be expressed exactly. – David Zhang Feb 25 '15 at 20:11
78

Primarily, rounding errors come from the fact that the infinity of all real numbers cannot possibly be represented by the finite memory of a computer, let alone a tiny slice of memory such as a single floating point variable, so many numbers stored are just approximations of the number they are meant to represent.

Since there are only a limited number of values which are not an approximation, and any operation between an approximation and an another number results in an approximation, rounding errors are almost inevitable.

The important thing is to realise when they are likely to cause a problem and take steps to mitigate the risks.

In addition to David Goldberg's essential What Every Computer Scientist Should Know About Floating-Point Arithmetic (re-published by Sun/Oracle as an appendix to their Numerical Computation Guide), which was mentioned by thorsten, the ACCU journal Overload ran an excellent series of articles by Richard Harris about the Floating Point Blues.

The series started with

Numerical computing has many pitfalls. Richard Harris starts looking for a silver bullet.

The dragon of numerical error is not often roused from his slumber, but if incautiously approached he will occasionally inflict catastrophic damage upon the unwary programmer's calculations.

So much so that some programmers, having chanced upon him in the forests of IEEE 754 floating point arithmetic, advise their fellows against travelling in that fair land.

In this series of articles we shall explore the world of numerical computing, contrasting floating point arithmetic with some of the techniques that have been proposed as safer replacements for it. We shall learn that the dragon's territory is far reaching indeed and that in general we must tread carefully if we fear his devastating attention.

Richard starts by explaining the taxonomy of real numbers, rational, irrational, algebraic and transcendental. He then goes on to explain IEEE754 representation, before going on to cancellation error and order of execution problems.

If you read no deeper than this, you will have an excellent grounding in the problems associated with floating point numbers.

If you want to know more however, he continues with

He then switches to trying to help you cure your Calculus Blues

and last but not least, there is

The whole series of articles are well worth looking into, and at 66 pages in total, they are still smaller than the 77 pages of the Goldberg paper.

While this series covers much of the same ground, I found it rather more accessible than Goldberg's paper. I also found it easier to understand the more complex parts of the paper after reading the earlier of Richards articles and after those early articles, Richard branches off into many interesting areas not touched on by the Goldberg paper.

As thus spake a.k. mentioned in comments:

As the author of those articles I'd like to mention that I have created interactive versions of them on my blog www.thusspakeak.com starting with thusspakeak.com/ak/2013/06.

Community
  • 1
Mark Booth
  • 14,214
  • 3
  • 40
  • 79
  • 1
    As the author of those articles I'd like to mention that I have created interactive versions of them on my blog www.thusspakeak.com starting with https://www.thusspakeak.com/ak/2013/06/. – thus spake a.k. Apr 03 '19 at 16:02
  • Thanks @thusspakea.k. I've added a note to my answer, and those interactive elements work very nicely. – Mark Booth Apr 03 '19 at 16:24
12

Well, thorsten has the definitive link. I would add:

Any form of representation will have some rounding error for some number. Try to express 1/3 in IEEE floating point, or in decimal. Neither can do it accurately. This is going beyond answering your question, but I have used this rule of thumb successfully:

  • Store user-entered values in decimal (because they almost certainly entered it in a decimal representation - very few users will use binary or hex). That way you always have the exact user-entered representation.
  • If you have to store user-entered fractions, store the numerator and denominator (also in decimal)
  • If you have a system with multiple units of measure for the same quantity (like Celsius/Fahrenheit), and the user can enter both, store the value they entered and the units they entered them in. Don't try to convert and save as a single representation, unless you can do it without loss of precision/accuracy. Use the stored value and units in all calculations.
  • Store machine generated values in IEEE floating point (this can be numbers generated by an electronic measurement device, like an analog sensor with an A/D converter, or the unrounded result of a calculation). Note that this doesn't apply if you're reading a sensor over a serial connection and it's already giving you the value in a decimal format (e.g. 18.2 C).
  • Store user-viewable totals, etc., in decimal (like a bank account balance). Round appropriately, but use that value as the definitive value for all future calculations.
Community
  • 1
Scott Whitlock
  • 21,874
  • 5
  • 60
  • 88
  • I would add: Consider using an arbitrary-precision math package like ARPREC or decNumber. – Blrfl Aug 15 '11 at 14:58
  • I don't decimal (as opposed to binary) has much benefit for integer values, such as the numerator and denominator of a fraction. Either can store exact integer values, and binary is more efficient. There's some cost in converting back and forth for input and output, but that's likely to be swamped by the cost of physically performing the I/O. – Keith Thompson Jan 27 '12 at 20:35
11

What seems to have not been mentioned so far are the concepts of an unstable algorithm and an ill-conditioned problem. I'll address the former first, as that seems to be a more frequent pitfall for novice numericists.

Consider the computation of the powers of the (reciprocal) golden ratio φ=0.61803… ; one possible way to go about it is to use the recursion formula φ^n=φ^(n-2)-φ^(n-1), starting with φ^0=1 and φ^1=φ. If you run this recursion in your favorite computing environment and compare the results with accurately evaluated powers, you'll find a slow erosion of significant figures. Here's what happens for instance in Mathematica:

ph = N[1/GoldenRatio];  
Nest[Append[#1, #1[[-2]] - #1[[-1]]] & , {1, ph}, 50] - ph^Range[0, 51]  
{0., 0., 1.1102230246251565*^-16, -5.551115123125783*^-17, 2.220446049250313*^-16, 
-2.3592239273284576*^-16, 4.85722573273506*^-16, -7.147060721024445*^-16, 
1.2073675392798577*^-15, -1.916869440954372*^-15, 3.1259717037102064*^-15, 
-5.0411064211886014*^-15, 8.16837916750579*^-15, -1.3209051907825398*^-14, 
2.1377864756200182*^-14, -3.458669982359108*^-14, 5.596472721011714*^-14, 
-9.055131861349097*^-14, 1.465160458236081*^-13, -2.370673237795176*^-13, 
3.835834102607072*^-13, -6.206507137114341*^-13, 1.004234127360273*^-12, 
-1.6248848342954435*^-12, 2.6291189633497825*^-12, -4.254003796798193*^-12, 
6.883122762265558*^-12, -1.1137126558640235*^-11, 1.8020249321541067*^-11, 
-2.9157375879969544*^-11, 4.717762520172237*^-11, -7.633500108148015*^-11, 
1.23512626283229*^-10, -1.9984762736468268*^-10, 3.233602536479646*^-10, 
-5.232078810126407*^-10, 8.465681346606119*^-10, -1.3697760156732426*^-9, 
2.216344150333856*^-9, -3.5861201660070964*^-9, 5.802464316340953*^-9, 
-9.388584482348049*^-9, 1.5191048798689004*^-8, -2.457963328103705*^-8, 
3.9770682079726053*^-8, -6.43503153607631*^-8, 1.0412099744048916*^-7, 
-1.6847131280125227*^-7, 2.725923102417414*^-7, -4.4106362304299367*^-7, 
7.136559332847351*^-7, -1.1547195563277288*^-6}

The purported result for φ^41 has the wrong sign, and even earlier, the computed and actual values for φ^39 share no digits in common (3.484899258054952*^-9for the computed version against the true value7.071019424062048*^-9). The algorithm is thus unstable, and one should not use this recursion formula in inexact arithmetic. This is due to the inherent nature of the recursion formula: there is a "decaying" and "growing" solution to this recursion, and trying to compute the "decaying" solution by forward solution when there is an alternative "growing" solution is begging for numerical grief. One should thus ensure that his/her numerical algorithms are stable.

Now, on to the concept of an ill-conditioned problem: even though there may be a stable way to do something numerically, it may very well be that the problem you have just cannot be solved by your algorithm. This is the fault of the problem itself, and not the solution method. The canonical example in numerics is the solution of linear equations involving the so-called "Hilbert matrix":

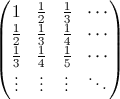
Hilbert matrix

The matrix is the canonical example of an ill-conditioned matrix: trying to solve a system with a large Hilbert matrix might return an inaccurate solution.

Here's a Mathematica demonstration: compare the results of exact arithmetic

Table[LinearSolve[HilbertMatrix[n], HilbertMatrix[n].ConstantArray[1, n]], {n, 2, 12}]
{{1, 1}, {1, 1, 1}, {1, 1, 1, 1}, {1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 
  1}, {1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1,
   1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 
  1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}

and inexact arithmetic

Table[LinearSolve[N[HilbertMatrix[n]], N[HilbertMatrix[n].ConstantArray[1, n]]], {n, 2, 12}]
{{1., 1.}, {1., 1., 1.}, {1., 1., 1., 1.}, {1., 1., 1., 1., 1.},  
  {1., 1., 1., 1., 1., 1.}, {1., 1., 1., 1., 1., 1., 1.}, 
  {1., 1., 1., 1., 1., 1., 1., 1.}, {1., 1., 1., 1., 1., 1., 1., 1., 1.},  
  {1., 1., 1., 0.99997, 1.00014, 0.999618, 1.00062, 0.9994, 1.00031, 
  0.999931}, {1., 1., 0.999995, 1.00006, 0.999658, 1.00122, 0.997327, 
  1.00367, 0.996932, 1.00143, 0.999717}, {1., 1., 0.999986, 1.00022, 
  0.998241, 1.00831, 0.975462, 1.0466, 0.94311, 1.04312, 0.981529, 
  1.00342}}

(If you did try it out in Mathematica, you'll note a few error messages warning of the ill-conditioning appearing.)

In both cases, simply increasing the precision is no cure; it will only delay the inevitable erosion of figures.

This is what you might be faced with. The solutions might be difficult: for the first, either you go back to the drawing board, or wade through journals/books/whatever to find if somebody else has come up with a better solution than you have; for the second, you either give up, or reformulate your problem to something more tractable.

I'll leave you with a quote from Dianne O'Leary:

Life may toss us some ill-conditioned problems, but there is no good reason to settle for an unstable algorithm.

9

because base 10 decimal numbers cannot be expressed in base 2

or in other words 1/10 cannot be transformed into a fraction with a power of 2 in the denominator (which is what floating point numbers essentially are)

ratchet freak
  • 25,706
  • 2
  • 62
  • 97
  • 12
    Not exactly true: 0.5 and 0.25 can be expressed in base 2. I think you mean "not all base 10 decimal numbers". – Scott Whitlock Aug 15 '11 at 14:29
  • 3
    More accurately. Not all fractional numbers can be represented exactly using a floating point notation (ie with the . Both base 2 and base 10 have this exact problem). Try and do `9*3.3333333` in decimal and comapre it to `9*3 1/3` – Martin York Aug 15 '11 at 14:42
  • 1
    This is the most common source of floating-point confusion. `.1 + .1 != .2` because floating-point binary encoding is used, not decimal. – Sean McMillan Aug 16 '11 at 11:50
  • @SeanMcMillan: And `1.0/3.0*3.0 != 1.0`, because floating-point binary encoding is used, not trinary. – Keith Thompson Mar 04 '13 at 16:10
9

In mathematics, there are infinitely many rational numbers. A 32 bit variable can only have 232 different values, and a 64 bit variable only 264 values. Therefore, there are infinitely many rational numbers that have no precise representation.

We could come up with schemes that would allow us to represent 1/3 perfectly, or 1/100. It turns out that for many practical purposes this isn't very useful. There's one big exception: in finance, decimal fractions often do pop up. That's mostly because finance is essentially a human activity, not a physical one.

Therefore, we usually choose to use binary floating point, and round any value that can't be represented in binary. But in finance, we sometimes choose decimal floating point, and round values to the closest decimal value.

MSalters
  • 8,692
  • 1
  • 20
  • 32
  • 2
    Even worse, while an infinite (countably infinite) amount of memory would enable one to represent all of the rationals, it would not suffice for representing the reals. Even worse yet, almost all of the real numbers are not computable numbers. The best we can do with a finite amount of memory is to approximate a finite range subset of the reals. – David Hammen Aug 15 '11 at 14:18
  • @David - with infinite memory, we could represent all the real numbers that can be named. – kevin cline Aug 15 '11 at 14:41
  • 4
    @Kevin: You're talking about the computable numbers, which is a tiny subset (a subset with measure zero) of the reals. – David Hammen Aug 15 '11 at 15:08
  • 1
    +1 for the most basic explanation: You're trying to represent an infinite amount of numbers with a finite number of bits. – Raku Aug 15 '11 at 16:00
  • 1
    @DavidHammen: Computable numbers are a tiny subset (of measure zero) of the reals -- but every number you'll ever work with in a program is, by definition, computable. – Keith Thompson Jan 27 '12 at 20:37
  • @Keith Thompson: This does not contradict the assertion that you cannot represent all real numbers in a computer (you cannot work with certain numbers), i.e. that rounding errors are inevitable. – Giorgio Mar 04 '13 at 12:26
  • @Giorgio: No, and I didn't say it did. But you could come up with a scheme that can represent all computable numbers (at tremendous cost in time and storage), and that would suffice for any computation a computer can perform. And if you restrict yourself to `+`, `-`, `*`, and `/`, arbitrary-precision rationals avoid rounding errors -- at considerable cost, again, in time and storage. – Keith Thompson Mar 04 '13 at 16:14
  • @Keith Thompson: Ok, I understand what you mean. I meant that you must have rounding errors as soon as you try to represent arbitrary real numbers like the square root of 2. But if you restrict yourself to representable numbers, then I think I understand what you mean. – Giorgio Mar 04 '13 at 17:02
  • 3
    @Giorgio: If you choose the right representation, the square root of 2 *is* representable, for example, as the string `"√2"`. (My old HP-48 calculator was able to do exactly that, and squaring that value resulted in exactly `2.0`.) There are only a countable infinity of representable real numbers for *any* finite representation -- but no computation can yield a number that is not, in principle, representable. In practice, binary floating-point drastically limits the set of representable numbers, with the benefit of blazing speed and tiny storage relative to symbolic representations. – Keith Thompson Mar 04 '13 at 18:29
-2

the only really obvious "rounding issue" with floating-point numbers i think about is with moving average filters:

$$\begin{align} y[n] & = \frac{1}{N}\sum\limits_{i=0}^{N-1} x[n-i] \ & = y[n-1] + \frac{1}{N}(x[n] - x[n-N]) \ \end{align}$$

to make this work without the buildup of noise, you want to make sure that the $x[n]$ you add in the current samples is precisely the same as the $x[n-N]$ you will subtract $N$ samples into the future. if it is not, then what is different is a little turd that gets stuck in your delay line and will never come out. that is because this moving average filter is actually built with an IIR that has a marginally stable pole at $z=1$ and a zero that cancels it inside. but, it's an integrator and any crap that gets integrated and not entirely removed will exist in the integrator sum forevermore. this is where fixed-point does not have the same problem that floating-point numbers do.

robert bristow-johnson
  • 1,190
  • 1
  • 8
  • 17