How does one design an op amp circuit which calculates the logarithm of the incoming voltage? I.E. if \$V_{in}\$ is the voltage at the input of the circuit and \$V_{out}\$ is the voltage at the output of the circuit, then the relationship between the two should be $$ V_{out}=\log_{10}\left(\frac{V_{in}}{V_{ref}}\right), $$ where \$V_{ref}\$ is some reference voltage such as 1 V.
Asked
Active
Viewed 95 times
1
-
Application note 31 says? – Ignacio Vazquez-Abrams Jan 26 '14 at 05:09
-
I hope you don't remove this question as a duplicate. My question is specifically about an op amp circuit, which is indeed very similar to the question linked, but @SpehroPefhany gave an answer which more specifically addresses my question. – Chris Mueller Jan 26 '14 at 15:50
-
@IgnacioVazquez-Abrams I don't follow. – Chris Mueller Jan 26 '14 at 15:51
-
Only because you haven't looked at it. – Ignacio Vazquez-Abrams Jan 26 '14 at 16:02
-
@IgnacioVazquez-Abrams I take it you are referring to [this document from National Semiconductor?](http://www.ti.com/ww/en/bobpease/assets/AN-31.pdf) See what I did there? Thats called a link. Regardless of the snarkiness, this is a very useful document, and I appreciate you pointing me towards it. – Chris Mueller Jan 26 '14 at 16:12
1 Answers
1
For a BJT, \$V_{BE} \approx\$ \$V_T \cdot ln(\$ \$ I_c \over I_S\$), where \$V_T = \$\$k \cdot T\over q\$, and \$I_S \$ is a transistor characteristic (saturation current).
So, it's a matter of scaling to get what you're asking for.
Recall that \$log_{10}(x)\$ = \$ ln(x)\over ln(10) \$.
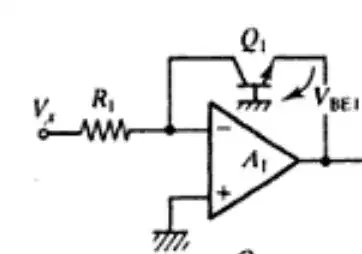
The devil is in the details, however, and both \$I_S\$ and \$ V_T\$ are temperature dependent, so compensation is required, perhaps with a temperature-dependent resistance.
See this answer.
Spehro Pefhany
- 376,485
- 21
- 320
- 842