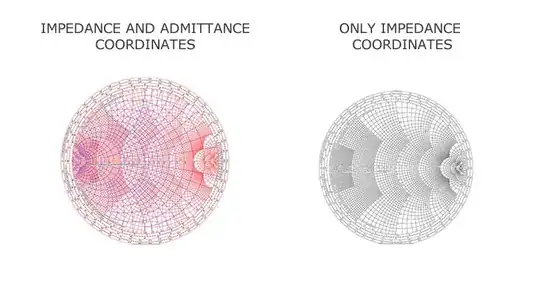
There are Smith charts with impedance and admittance coordinates and Smith charts with only impedance coordinates.
I believe I learned how to use the first one. Is there any sense in studying how to use the second one?
There are Smith charts with impedance and admittance coordinates and Smith charts with only impedance coordinates.

I believe I learned how to use the first one. Is there any sense in studying how to use the second one?
Learning to use the chart on the right, by itself, is a good academic exercise but not very useful.
When using the YZ-chart on the left, the top half is inductive and the bottom half is capacitive. This is true for both series and parallel components. When the Z-chart on the right is used to draw admittance curves, everything is reversed. The top half is capacitive and the bottom is inductive. This is why a series inductor and a shunt capacitor follow the same path. It just adds unnecessary confusion.
The usage is exactly the same. Impedance \$Z\$ and admittance \$Y\$ are the same thing, described differently:
$$ Y \equiv \frac{1}{Z} $$
Adding the admittance lines to the chart just makes it easier to use in many cases. For example, when adding a parallel reactive component to the matching network you will move around the admittance circles. When the lines aren't drawn, as in the "impedance only" example, the same thing happens, but the lines aren't there to help you see.