Current divider rule calculation issue

Question

I'm doing the exercises from Wisc-Online. This one

I think they are really great to learn and practice and have already done a bunch of their practical trainings. But here I'm starting to be crazy. I need to calculate \$I_{r1}\$

Here's the schema :

^{simulate this circuit – Schematic created using CircuitLab}

According to their lesson :

\$I_{Rx} = \dfrac{R_{T}}{R_{x}} \times I_{T}\$

So :

\$I_{R1} = \dfrac{R_{1} \parallel R_{2}}{R_{1}} \times I_{T}\$

With values :

\$I_{R1} = \dfrac{\dfrac{1}{\cfrac{1}{5000}+\cfrac{1}{10000}}}{\dfrac{1}{5000}} \times 3mA\$

\$I_{R1} = 50000mA\$

But the answer should be 2mA

What's wrong in my formula ? :'(

Answer 1

Sorry... I just figured out what was wrong... It's not :

\$I_{R1} = \dfrac{\dfrac{1}{\cfrac{1}{5000}+\cfrac{1}{10000}}}{\dfrac{1}{5000}} \times 3mA\$

But :

\$I_{R1} = \dfrac{\dfrac{1}{\cfrac{1}{5000}+\cfrac{1}{10000}}}{5000} \times 3mA\$

And in that case I've got the correct answer.

Sorry.

Answer 2

Learn to recognize the simple cases. It will make your life easier.

You have two resistors in parallel. With current flowing through the combination, there's a voltage across the combination. Looking at the voltage across the combination, and noticing that one resistor is half the value of the other, it immediately follows that the \$5k\Omega\$ resistor will carry twice as much current as the \$10k\Omega\$ resistor.

\$I_{R_{1}} + I_{R_{2}} = 3 mA \$

However, \$I_{R_{1}} = 2 \times I_{R_{2}}\$

So \$3 \times I_{R_{2}} = 3 mA\$

And that gives you \$I_{R_{2}} = 1 mA\$ and then \$I_{R_{1}} = 2 mA\$.

Answer 3

The general formula for a current divider is a lot easier to remember in terms of conductance/admittance than instead of resistance/impedance. These are inverses of each other, e.g. the conductance \$G\$ of a resistor is \$\frac{1}{R}\$. Then it is the same exact analogue of the formula for a voltage divider:

$$ I_k = \frac{G_k}{G_\text{total}}I_{\text{total}} $$

For a two-resistor network that's:

$$ I_1 = \frac{\frac{1}{R_1}}{\frac{1}{R_1}+\frac{1}{R_2}}I_{\text{total}} = \frac{{R_2}}{{R_1}+{R_2}}I_{\text{total}}$$

For two resistors, the conductance form requires a few more computations (two more inversions) than the simplified form, but is easier to not get wrong. The thing to remember so that you get the final formula right is that unlike a voltage divider where the greatest voltage drop is across the larger resistor, for a current divider the larger current flows through the smaller resistor (which has larger conductance). Another way to remember it right is to check what happens if you put a resistor in parallel with a short circuit; then you expect no current to flow through the non-zero resistor. So if \$R_2 = 0\$ then you expect \$I_1 = 0\$.

Alas, the formula on the extreme right doesn't generalize as-is to more resistors. For three resistors it becomes much more nasty if you try to eliminate the reciprocals:

And speaking of that Wisconsin problem set, for a problem like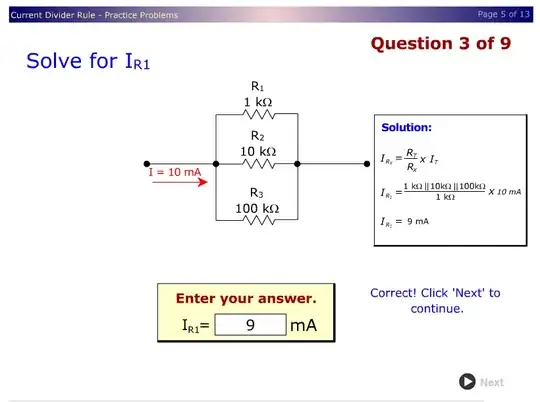

you could calculate the first current the hard way (it's actually 9.009009... mA) or just guesstimate it as 90% of the total (by ignoring the large, bottom resistor) but for the subsequent questions like the current through the next (and then final) resistors,

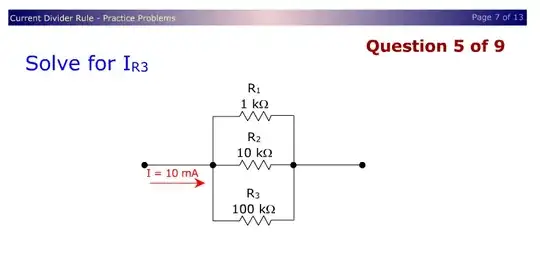
if you remember the idea about proportionality with the conductance in a current divider, then knowing the current through \$R_1\$ immediately gives you the current through the others by division, e.g. \$R_2\$ is ten times larger than \$R_1\$, so the current through it is going to be ten times smaller and for \$R_3\$ it will be 100 times smaller.

Answer 4

Assume the total current as it is = 3 mA (From the picture above). This current divided itself into the two resistors R1 and R2 and name the two currents as I1 and I2 successively. From the ohm law, we know that the voltage drop across the two different resistors but put in parallel structure will have the same voltage drop and called it V = I1 * R1 = I2 * R2. We know from the Kirchoff law that It = I1 + I2 or I1 = It - I2 or I2 = It - I1, then we can find the current that flows through each resistor by using the following formula,

I1= I2 * R2/(R1);I1 = (It-I1) * R2/(R1);I1 * R1 = It * R2-I1*R2;I1(R1+R2)=ItR2;I1=ItR2/(R1+R2).

By using the same logic to the above formula we can find that I2=It*R1/(R1+R2).

Now with It=3mA, we can find I1=3mA*(10Kohm)/(15Kohm)=2mA, and I2=3mA(5Kohm)/(15Kohm)=1mA. The voltage drop across the two resistors R1 and R2 are I1R1=I2*R2;2mA*5Kohm=1mA*10Kohm=10Volt. It can be seen clearly that the two voltage drop across the two resistors is the same (10 V). The total current is I1+I2=2mA+1mA=3mA.