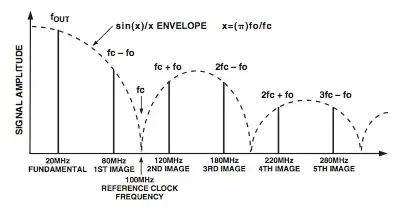
When looking at AD9850 DDS or other similar parts made by Analog Devices, it is obvious that the output signal amplitude changes with frequency. This can be shown as \$x= \pi \dfrac{f_{out}}{f_{clock}}\$ and amplitude changes by \$\dfrac{\sin x }{x}\$.
Using this formula, we should see an amplitude drop less that 20% between 1Hz to 50 MHz but this is not the case .
As I am driving this part, I see the amplitude is around 1 volt pk-pk at 10Hz and 10mV at 50 MHz. Am I missing something in these calculations?