Maximum power transfer

Question

I have problems to solve the next exercise about maximum power transfer.

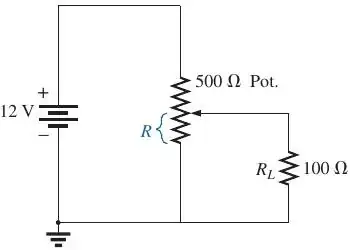
I know that potentiometer has two internal resistors. In this exercise, I must find the \$R\$ value to transfer maximum power to \$R_{L}\$. Now, I have two ideas:

• To consider \$R = 500\Omega\$. If I perform it and then get Thévenin equivalent, simply \$R_{th} = 0\Omega\$ and \$V_{th} = 12V\$. Here I can't use the formula: $$ P_{max} = \frac{V_{th}^2}{4R_{th}}$$

  but the transferred power to \$R_{L}\$: $$ P_{R_{L}}= \frac{(12V)^2}{100\Omega} = 1.44W$$

• To assume \$500\Omega = R + R_{1}\$. In this case (\$R_{1}\$ is the other potentiometer resistor), \$R_{th} = R||R_{1} = R_{L}\$ (based on maximum power transfer theorem). I solve a quadratic equation and: $$R = (250 \pm 50\sqrt{5})\Omega\\V_{th} = \frac{12R}{500}V$$ and implies two different Thévenin voltages. Performing power calculations, I get: $$P_{R_{L}} = 36(3\pm\sqrt{5})mW$$

Definitely, the first approach gives a higher power (and suppose it's maximum power transferred by the source) , but which is correct?

Answer 1

The problem as described has a trivial solution. To maximize the power into the \$100 \Omega\$ load, the pot should be turned to one end so that \$R = 500 \Omega\$. Then the \$12V\$ source appears entirely across the load and delivers \$\dfrac{12^2}{100}\$ or \$1.44 W\$. The maximum power theorem applies when the source impedance is fixed and the load is variable, which is not the case here.

Answer 2

Barry gives the correct answer. What follows is the mathematical justification.

The power delivered to the load resistor, for a given Thevenin equivalent circuit is:

\$P_L = V_L \cdot I_L = V_{th}\dfrac{R_L}{R_{th}+ R_L} \cdot \dfrac{V_{th}}{R_{th}+ R_L} = V^2_{th} \dfrac{R_L}{(R_{th}+ R_L)^2}\$

If we fix \$R_{th}\$ and ask which value for \$R_L\$ gives maximum \$P_L\$, the value is given by \$R_L = R_{th}\$ and the resulting power delivered to the load is:

\$P_{L,max} = \dfrac{V^2_{th}}{4R_{th}} \$

However, if we fix \$R_L \$, and ask which value for \$R_{th}\$ gives maximum \$P_L\$, the answer is, by inspection, \$R_{th} = 0\$.

Thus, the answer is \$R = 500 \Omega \$ so that \$R_{th} = 0\$