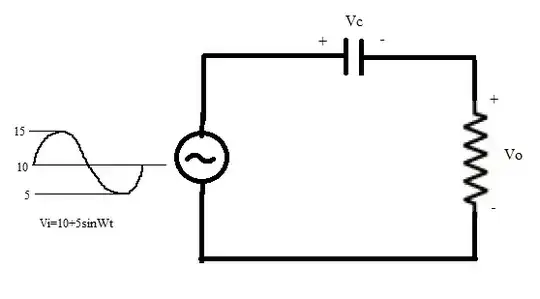
This question has been in my head for so many days. When I was studying BJT amplifiers, capacitors were used for blocking DC. It is called a coupling capacitor. When the AC signal is superimposed on DC and is applied to the circuit shown, what would be output across R(Vo)? My professor told that we will get a sine wave(5sinWt) with reference to ground and DC(10) would be eliminated. But I am not able to visualize the waveforms across C and R. I want to know how capacitor charges and discharges and blocks dc. Please help me with the waveforms.