Why does the thickness of a wire affect resistance?

Question

A teacher explained why by using a highway analogy. The more lanes you have, the faster the cars go through, where the number of lanes obviously represent the wire thickness and the cars represent electrons. Easy enough.

But after a certain point shouldn't the wire get so thick, that any thickness after that doesn't affect resistance? For example, if you have a 100 cars going down a highway, a 4 lane highway is going to allow the cars to move a lot faster than a 1 lane one, because there are a fewer cars per lane. But a 1000 lane highway highway is going to be as efficient as a 10000 lane one, because on both highways every car has its own lane. After a 100 lanes, the number of lanes doesn't provide resistance.

So why does increasing wire thickness always decrease resistance?

Answer 1

The car analogy isn't such a good one, since electrons don't actually flow from one end of the wire to the other (well they do but extremely slowly) and it implies there is some space between the cars, whereas it would be more like a traffic jam whatever the width of the highway.
It's more like a line of billiard balls, and force is applied to the first one, and the energy is transferred to the last one through all the intermediate balls (a bit like newtons cradle, although the balls don't really bounce into each other). The free electrons bounce around, occasionally being impeded (see below) with the potential difference causing an average inclination to the direction of current.

A water analogy is better - the pipe is always full of water, and for the same pump (battery), the pressure (voltage) is always lower the wider the pipe, which equates to more flow and a lower resistance.

This quote from the Wiki page on resistivity explains reasonably well:

In metals - A metal consists of a lattice of atoms, each with an outer shell of electrons which freely dissociate from their parent atoms and travel through the lattice. This is also known as a positive ionic lattice.4
This 'sea' of dissociable electrons allows the metal to conduct electric current. When an electrical potential difference (a voltage) is applied across the metal, the resulting electric field causes electrons to move from one end of the conductor to the other.
Near room temperatures, metals have resistance. The primary cause of this resistance is the thermal motion of ions. This acts to scatter electrons (due to destructive interference of free electron waves on non-correlating potentials of ions)[citation needed]. Also contributing to resistance in metals with impurities are the resulting imperfections in the lattice. In pure metals this source is negligible[citation needed].
The larger the cross-sectional area of the conductor, the more electrons per unit length are available to carry the current. As a result, the resistance is lower in larger cross-section conductors. The number of scattering events encountered by an electron passing through a material is proportional to the length of the conductor. The longer the conductor, therefore, the higher the resistance. Different materials also affect the resistance.

Answer 2

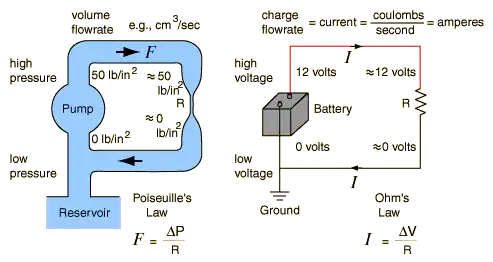
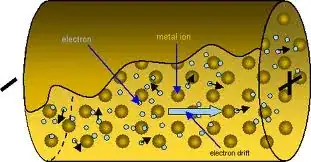
I'm going to approach your question in a slightly different way to try and give you a slightly more intuitive understanding of why the resistance goes down.

Let's first consider the equivalent resistance of a simple circuit:

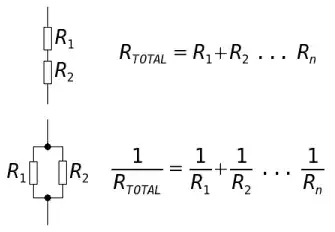
_{(source: electronics.dit.ie)}

When resistors are in parallel (bottom circuit in picture), the total resistance is: \$\frac{1}{R_{Total}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} ... \frac{1}{R_n} \$

You can see this equation in a textbook, but you might be wondering "But you added more resistors! How could that make the resistance go down?".

To understand why, let's look at electrical conductance. Conductance is the inverse of resistance. That is, the less resistive a material is, the more conductive it is. Conductance is defined as \$G = \frac{1}{R}\$ where \$G\$ is the conductance and \$R\$ is the resistance.

Now this part is interesting, look what happens when we use conductance in the parallel circuit resistance equation.

\$Conductance = G_{Total} = G_1 + G_2 + G_3 .. G_n = \frac{1}{R_{Total}}= \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} ... \frac{1}{R_n} \$

We see here that conductance increases as you add more resistors in parallel, and resistance decreases! Each resistor is able to conduct a certain amount of current. When you add a resistor in parallel, you are adding an additional path through which current can flow, and each resistor contributes a certain amount of conductance.

When you have a thicker wire, it effectively acts like this parallel circuit. Imagine you have a single strand of wire. It has a certain conductance and a certain resistance. Now imagine you have a wire that is composed of 20 individual strands of wire, and each strand is as thick as your previous single strand.

If each strand has a certain conductance, having a wire with 20 strands means that your conductance is now 20 times larger than the wire with only 1 strand. I'm using strands because it helps you see how a thicker wire is the same as having multiple smaller wires. Since the conductance increases, it means the resistance decreases (since it is the inverse of conductance).

Answer 3

Electricity is nothing but the flow of electrons through a material. In one way, it's like a garden hose already full of water. When the water turned on (pressure applied) at the faucet, the pressure travels through the hose much faster than any particular water molecule, and water begins flowing out of the far end nearly immediately. A wire is chock full of electrons able to move when you apply a bit of electromotive force. Apply a voltage, and you don't have to wait for the first electrons in to traverse the wire, they start moving at the far end almost immediately.

Now think of a cross section of the wire . . . imagine drawing a line around the wire, perpendicular to the axis of the wire. Now imagine counting the number of electrons passing this line, through the circle that is the cross section of the wire. This is the current, measured in amps. There are a couple of ways you can have the same current. Lots of electrons drifting slowly by, or fewer electrons hauling a&& to get the same number passing through your cross section per second, and hence the same current.

How do you convince them to move faster? Apply a greater electromotive force. So in a wire with half the diameter, you'd have one fourth the cross-sectional area, which means one fourth the number of electrons available in any given length of wire to pass your line per second. What'cha gonna do to get that current up with fewer electrons available to move? You're gonna have to move them faster so that the same number can pass by per second by applying a higher voltage.

There you have it: A thinner wire requires a higher voltage to carry the same current. That's pretty much the definition of resistance, since V/I = R.

Answer 4

Forget the highway analogy. The resistance of a wire depends on 3 parameters: the conductivity of the material from which the wire is made, its cross sectional area, and its length. Highly conductive materials, such as copper and silver, are used to manufacture wire to achieve a low resistance. The longer a wire is the more resistance it has due to the longer path the electrons have to flow along to get from one end to the other. The larger the cross sectional area, the lower the resistance since the electrons have a larger area to flow through. This will continue to apply no matter how thick the wire is. The electron flow will adjust itself to whatever the wire thickness is.

Answer 5

A teacher explained why by using a highway analogy. The more lanes you have, the faster the cars go through, where the number of lanes obviously represent the wire thickness and the cars represent electrons. Easy enough.

What teacher should have said is :

• Assume that cars travel at a constant speed and with constant spacing on a highway lane.
• The amount of vehicles going past a point will be proportional to the number of lanes.
• Increasing the number of lanes does not increase the speed of the vehicles. (Not quite true because cars are driven by people!)

Answer 6

This is a great question! - The highway / car is an excellent analogy

In this analogy, you have to consider these factors.

Your design will have a requirement for voltage - in our model, voltage is the SPEED the cars need to travel.

The design will have a requirement for current - the is the NUMBER OF CARS needed to travel down the highway. (or volume)

The wire size / resistance is the NUMBER OF LANES.

Wattage, or power, is the combination of both voltage * current, or the number of cars travelling down the highway in a given time.

The highway has to be designed to meet the specifications for both speed and volume. If you have a very small current requirement, say, 1 car, you'll only ever need a one lane highway, because your can can travel as fast as possible, (high voltage). But if you have a high current requirement, 10,000 cars, you'll need a 100 lane highway. (depending on power requirements)

But take for example, the power grid - a transmission line for a city of 1 million people. That is very roughly 300,000 households, each using 1 kw of power. That means our line needs to deliver 3 Gigawatts of power! You could do this with 1 V @ 3 giga-amps, or 3 GV @ 1 amp, or something in between.

What voltage / current would be required to make the transmission line as small as possible?

Answer 7

Do you know why doesn't the car analogy works fine? Even if we disregarded the possibility that electrons don't really actually move, you'd thing about them again as cars but not moving in straight lines! They move in a random zig zag paths. Therefore; the more lines the less possibility the cars will ever collide even with a zig zag path.

So you tacitly assumed electrons move in staright lanes (lines) just like cars, which in that case your assumption that the thickness of the wire won't affect. On the other hand, considering the cars to move in a non-straight lines, your assumed hypothesis won't fit your conclusion.