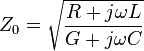2

As much as I know, the input impedance of a coaxial cable with a characteristic impedance of 50 \$\Omega\$ which is terminated with a 50 \$\Omega\$ load resistor, should be 50 \$\Omega\$ as well. This should be true for any cable length and any wavelength.

However, in a typical datasheet of any coaxial cable the capacitance of the cable per unit length is usually given. I don't understand the effect of this capacitance on the input impedance.

Assuming I have 10m length of a standard 50 \$\Omega\$ RG-58 coaxial cable terminated with a 50 \$\Omega\$ resistor. The capacitance of this cable is 100pF/m. What would be the input impedance?

Vadim
  • 69
  • 1
  • 8
  • Related: [How can PCB trace have 50 ohm impedance regardless of length and signal frequency?](http://electronics.stackexchange.com/questions/75368/how-can-pcb-trace-have-50-ohm-impedance-regardless-of-length-and-signal-frequenc) – Phil Frost Aug 08 '13 at 21:14
  • http://home.mira.net/~marcop/ciocahalf.htm – Phil Frost Aug 08 '13 at 22:35

2 Answers2

3

This should be true for any cable length and any wavelength.

No, this is not true for any wavelength. At low frequencies (as in telephony/audio) the characteristic impedance is dominated by R and C: -

It approximates to \$\sqrt{\frac{R}{jwc}}\$ i.e. complex

At dc it is \$\sqrt{\frac{R}{G}}\$ i.e. resistive

And at RF frequencies it is \$\sqrt{\frac{jwL}{jwC}} = \sqrt{\frac{L}{C}}\$ i.e. resistive

However, in a typical datasheet of any coaxial cable the capacitance of the cable per unit length is usually given. I don't understand the effect of this capacitance on the input impedance.

Data sheets do tend to give the capacitance per unit length (without mentioning L/m) and if you know the characteristic impedance you can calculate what L per metre is: -

\${Z_o}^2 = \frac{L}{C}\$ therefore \$L= C\times{Z_o}^2\$ = 100\$e^{-12}\times 50\times 50 = 0.25\$ uH per metre.

What would be the input impedance?

The input impedance of RG-58 at RF frequencies will be 50\$\Omega\$ resistive because there are inductive and capacitive components that are in ratio as per the formulas above. This assumes you are correctly terminating the cable in 50\$\Omega\$

EDIT This is about where the turning points are between audio (complex) impedances and HF resistive impedances. For a start, here is a good spec for RG-58. Below are the salient points: -

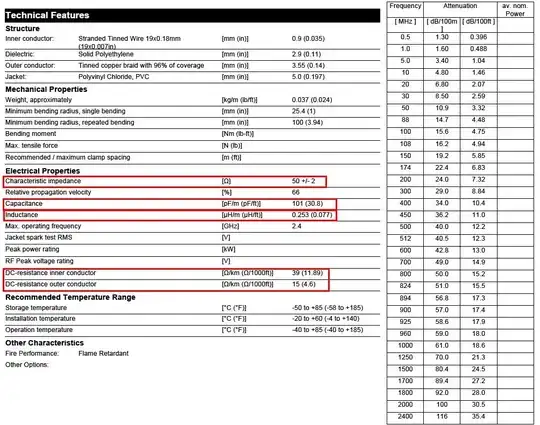
enter image description here

Notice the bottom two data highlighted in red - this is the inner and outer DC resistance per 1000ft - a total of 54\$\Omega\$ per 1000ft loop (304.8m). This equates to 0.1772\$\Omega\$ per metre.

For |jwL| to equal 0.1772, the frequency will be \$\frac{0.1772}{2\Pi L}\$ and if L = 0.25uH then F = 113kHz. Ten times higher in frequency (1.13MHz) and Zo pretty much approximates to \$\sqrt{\frac{L}{C}}\$ i.e. is 50\$\Omega\$ resistive.

For higher frequencies, Zo is a reliable resistive quantity, for frequencies down between 10kHz and 1MHz it's a mish-mash and at audio frequencies below 10kHz it becomes what is telephonically known as a "complex impedance" where the impedance is largely determined by series resistance and parallel capacitance and the impedance phase angle is about 45º because \$\sqrt{-j}\$ is 45 degrees.

Andy aka
  • 434,556
  • 28
  • 351
  • 777
  • At DC, it's resistive, then at "low" frequencies, it's complex, then at "RF" (higher frequencies), it becomes resistive again? How does that happen? – Phil Frost Aug 08 '13 at 22:19
  • @PhilFrost Do you mean formulaicly (spelling?) or physically? Not sure i can offer a decent answer on the physics side. The formula for Zo speaks for itself. Are you being serious about the formula side for Zo, a man of your knowledge and undoubted calibre? Maybe you are asking why the inductive side of things doesn't get going as early as the capacitive? If so, it toally depends on the cable dimensions - OK maybe a physics answer! – Andy aka Aug 08 '13 at 22:33
  • I never claimed to know everything :) It just seems counter-intuitive, and the distinction between "low" and "high" frequencies seem rather arbitrary. I think the answer could use more clarity on how the frequency independent, \$\sqrt{L/C}\$ simplification requires \$j\omega L \gg R\$, and where that's true is "high" frequency. – Phil Frost Aug 08 '13 at 22:38
  • @PhilFrost I hear what you say – Andy aka Aug 08 '13 at 22:52
2

The characteristic impedance of a line is not the DC resistance of that line. The characteristic impedance is:

enter image description here

With the Capacitance being per unit length. FYI, search "characteristic impedance" on this site or Google for more answers. The common representation of a transmission line is:

enter image description here

You can see that there are complex parameters. Be assured that your line will have a 50 ohm impedance.

scld
  • 2,216
  • 15
  • 17