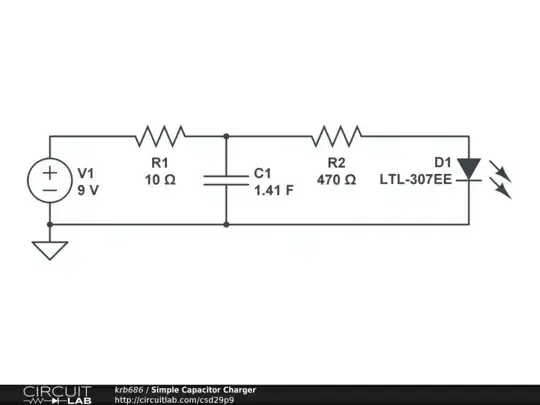
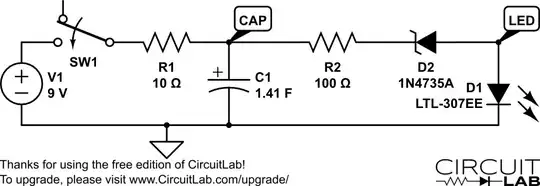
I've built this circuit to charge 3 large, .47F capacitors:

The capacitors are really big, and they charge up slowly. The addition of R2 and D is for D to light up in increasing power as the capacitors charge, and when they are fully charged, D should light up in full power.
However, I didn't manage to get it working correctly. D lights up in seamingly full power when the capacitors are not even half full.
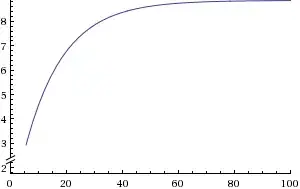
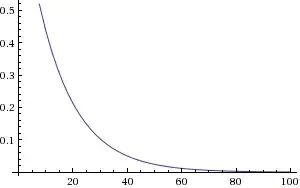
How can I create a V(t), I(t) and finally a R(t) functions for the capacitors? (It isn't an ohmic resistance but you get my point). Using these I'll be able to find proper values for R2 and D, and anyway I'm just intrested in how the voltage is built up.