Reducing the tolerance of resistors manually

Question

All the resistors available come with a finite amount tolerance. This is undesirable particularly in highly sensitive systems. While we can use resistors with the least tolerance available, I want to know if there are any methods (something like designing a special setup to bring down the tolerance) using which we can manually reduce the tolerance value to the minimum that we may require?

Without being too facetious, this is why resistors are available with different tolerances, down to 0.05%. The first "special" method would be to limit your searches with vendors to your design specification. — Scott Seidman, Jul 29 '13 at 14:27
You can count on a small nominal value of a resistor for a better accuracy — Dor, Jul 29 '13 at 15:33
If you cannot order the resistors to the tolerance you need, you could buy a whole bunch of the highest-tolerance resistors you can get, measure them all, and then only use the ones that meet your more-demanding tolerances. — AJMansfield, Jul 29 '13 at 19:47

Kaz · Accepted Answer · 2013-07-30T13:33:12.020

21

Tolerance is a statistical abstraction which tells us how much variation to expect from a sample of resistors of a given type. A single resistor doesn't have tolerance: it has a value, which deviates to some extent from the stated value (and of course varies with temperature). We cannot change (manually or otherwise) a property that a part doesn't have.

If part of a circuit requires a very accurately set resistance (which perhaps has to compensate for variations in other parts, and so cannot be a fixed value, no matter how precise), we can use a potentiometer. A potentiometer or rheostat is a resistor whose value you can manually change.

A useful trick is to use a fixed resistor for most of the resistance, and a smaller-valued potentiometer just for the adjustment. For instance, if we wanted to adjust 100K within a +/- 5% range, we could get a 95.3K resistor (E48 series number), and a 10K potentiometer wired as a rheostat in series with that resistor.

edited Jul 30 '13 at 13:33

answered Jul 29 '13 at 14:27

Kaz

19,838
1
39
82

Potentiometers tend to be "scratchy" as the wiper moves, which makes them not good for really low noise situations. – pjc50 Jul 29 '13 at 14:29
5

@pjc50 Not an issue for trimmer pots that are calibrated only a handful of times over their lifetime (perhaps once). – Kaz Jul 29 '13 at 14:33
5

Trimmer pots can have issues when used in high-vibration environments like cars, portable devices, etc. Not only can the "trim position" be shifted, but the wiper can also temporarily loose contact. Not a big deal for many applications, but shouldn't be ignored either. – Jul 29 '13 at 17:50
@DavidKessner In addition, some trimmer pots are garbage. I've seen catalog items rated for 25 turns! Adjust it 25 times and its life has come to an end; any further performance is a lucky bonus. – Kaz Jul 29 '13 at 18:54
@Kaz 95.3 is an E48 series value, not E24. E24 tops out at 910. – Anindo Ghosh Jul 30 '13 at 07:51
@AnindoGhosh Whoa, typo. E24 also tops out at two digits! – Kaz Jul 30 '13 at 13:32
@Kaz Yup, that's why I noticed the snafu :-) – Anindo Ghosh Jul 30 '13 at 13:33
@Kaz: Is the problem the number of times it can be adjusted, or the time part of the contact surface can go unused without oxidizing? The part of the contact surface that is being used at any exact moment probably won't oxidize, but if everything else does that could cause the next adjustment to render the part useless. – supercat Jul 30 '13 at 14:50

JIm Dearden · Answer 2 · 2013-07-30T09:10:19.517

12

While you cannot change the tolerance of the resistors you can select a value within the tolerance.

If you were to purchase say 1000 resistors and accurately measure their resistance values you may be able to find a few resistors that are closer to the actual value required. These selected resistors will effectively be very close tolerance resistors - even if they started life being bunched together with a lot of similar values. How 'close tolerance' they are would depend upon your test equipment.

Statistically speaking, however, there are no guarantees that within any sample size you will find exactly what your looking for.

edited Jul 30 '13 at 09:10

answered Jul 29 '13 at 15:14

JIm Dearden

18,926
30
40

Depending on the manufacturing process you may be out of luck with this approach. I measured about 50 10k 1% metal film resistors with an Agilent 34401A and most were some tens of ohms below the nominal value, just one came very close at 9998.5 Ohm. None were above 10k. I would guess they are trimmed (increasing resistance by cutting the metal film with a laser) until they are within the 1% tolerance. – starblue Jul 29 '13 at 16:20
1

@starblue like I said - statistically speaking, however, there are no guarantees that within any sample size you will find exactly what your looking for. – JIm Dearden Jul 29 '13 at 17:12
1

In one of my school labs (~ a dozen years ago) I tested several dozen relatively low tolerance resistors and found a bi-modal distribution just within the +/- tolerance values that looked as though the manufacturer had done equivalent testing to bin them. ex -5% to -4% or +4 to +5% deviations. – Dan Is Fiddling By Firelight Jul 29 '13 at 18:04
2

Its possible even that manufacturer already identified and pulled out all the resistors that meet higher tolerances, and subsequently labeled and sold them as such. – AJMansfield Jul 29 '13 at 19:51

Passerby · Answer 3 · 2020-02-23T03:26:42.107

You cannot reduce the tolerance of a resistor in this way, because Tolerance in this context, means fixed value from manufacturing. A given 10% resistor, given a steady current within a steady temperature range, will not swing from -10% to 1% to +10%, it will stay the same. (This goes out the window with time or with heat damage.) The Resistor tolerance simply means that the resistor should be within that range of the given value.

The way resistors tolerances are decided is that a batch is made and all parts are tested. In the E-12 (10%) and E-24 (5%) series, there is a close overlap between one "standard" resistor value and the next standard value up or down. Any resistor that is tested at more then 10% from the value it should be, gets labeled as the next value up or down. Any one that is only 5% or less, gets labeled as a 5% resistor, and anything between 10% and 5% is labeled as a 10% resistor. Any batch of 10% resistors you buy will most often than not, have no resistor in it that is within 5%. This means that a 1k 10% resistor in a given pack will be between 900 to 950, or 1050 to 1100, with the next value up being 1.2k 10%.

What you can do is part matching, where you test and measure multiple parts to find ones that are closely matched to each other. With the same 1k 10% resistor from above, you could find enough 930~950 resistors that they are essentially 940Ω 1% resistors. Not standard value of course, but given the small difference from the labeled value, it's an insignificant amount of current change. This is good enough for any situation where you need matched pairs, not precision value (Same goes for leds, the amount of brightness of an individual might not matter compared to making sure a set of ten leds have the same color and relative brightness.)

The OTHER OPTION though, is a bit more involved. Not complicated, but requires manual changes. This has been done for decades, especially if precision, non-standard values are needed. With carbon-film resistors, you take a file, and slowly break through the outer material and remove a tiny amount of the resistive material. This can increase the value, so that 1k 10% resistor that measures 950Ω can become 980Ω or 990Ω or exactly 1000Ω. You then use clear nail polish to seal it back up. This is what you were really asking about.

Resistor

http://www.youtube.com/watch?v=OQDjjIvLaj4

Are you sure about this process control for resistor manufacture described in your second paragraph? They're really manufactured tested, then binned? — Scott Seidman, Jul 29 '13 at 21:47
I suspect that the selection process mentioned in the second paragraph (if not an old technician's tale) may have been done with the old carbon composition resistors, but probably not with the current carbon or metal film variety. I once tested 50 or so Philips 5% 10K carbon and metal film resistors, and found a spread of about 1% between highest and lowest values. My Fluke meter showed the average slightly under 10K, so I concluded that my meter read slightly low. There was no sign that 1% or 2% resistors had been picked out of the 5% batch. — Peter Bennett, Jul 30 '13 at 02:18
@PeterBennett well, resistors tend to drift up, not down, that explains the low side tendencies. — Passerby, Jul 30 '13 at 02:57

score 3 · Answer 4 · answered Jul 29 '13 at 14:48

No, there is no way to "make" a more accurate resistor from a bunch of less accurate resistors.

For example, if you didn't think about it very hard you might be tempted to use four 10 kΩ 10% resistors in series/parallel configuration to make one 10 kΩ 5% resistor, but that doesn't work. If the values of the original resistors are randomly distributed over their range, then this method makes the resulting value more likely to be near nominal, but the maximum tollerance range is still exactly the same. Think of the limiting case where all resistors are 10% high. The result will also be 10% high regardless of how many you put together and average. Even the average is unlikely to get desirable results. When the circuit is assembled, you are likely to get a bunch of resistors from the same manufacturing batch, probably made immediately after each other. Such a distribution is not likely to be random. However, the point is the worst case error never gets better, which is what matters when designing a circuit.

If you want accurate resistance you either have to use accurate resistors or perform your own trimming.

One thing you can do is deal with the temperature range the resistor experiences. In the extreme case you could uses active heating and/or cooling to keep the resistor at a fixed temperature. That will decrease resistance drift due to temperature, but you still have the issue of the initial value.

There is no free lunch.

score 2 · Answer 5 · answered Jul 29 '13 at 15:06

2

First to know, tolerance includes several factors.

Maufacturing precision: resistors of same nominal are slightly different out of factory.
Stability against environment, such as temperature, humidity or pressure. Real value changes a bit when environment factors change.
Age stability. Value changes through time.
Noise

So they should be investigated before you improve a tolerance. First factor can be eliminated by selection through measurement of indiviual parts.

Second is an object for several engineering methods: place resistor to a more stable environment, isolate it from mechanical, sonic, thermic, electromagnetic influence and so on. Another way is to use more better material when manufacturing.

Third is the nature of materal, you can replace them, or tune he device after some time passes.

Fourth also depend on construction, temperature, current etc...

answered Jul 29 '13 at 15:06

Vovanium

987
8
10

`Third is the nature of materal, you can replace them, or tune he device after some time passes.` Do you mean that tuning the device can actually provide a better tolerance? If so, what are the methods available to do that? – TheLoneKing Jul 29 '13 at 15:48
I mean, after you tune a device for first time, then some period passed, you'll may have to tune it again. This is to aging of parts. – Vovanium Jul 29 '13 at 16:13
Note, tuning is also about to fight first factor (manufacturing precision). – Vovanium Jul 29 '13 at 16:15

score 1 · Answer 6 · answered Jul 29 '13 at 15:34

1

Turns out it is very tricky question and we need to be very cautious with terminology. First of all, lets put the term "tolerance" aside - the use of this term obscures the answers and raises terminology discussions.

Now, the best reference I found on the Web is this - an outstanding article about resistors' values.

Now, back to your concern. There is no way you can take "10% worst case" resistors and implement "5% worst case" resistor from them.

In applications which require really precise resistances you will do either of the following:

Add a trimmer to adjust the resistance
Measure the actual resistances and pick the components according to your needs
Add some sort of active component instead of simple resistor

However, in mass production the above approaches are (usually) too costly and time-consuming. It turns out that you might get to the point where the following decision will be made: we are not investing in ensuring that "worst case" scenario is of sufficient quality, but we do want 90% yield in sufficient quality.

In this case you may use techniques presented in the article I linked above to ensure that "on average" you resistors are closer to their nominal values. Then, of course, you'll have to test your final product and dispose the bad 10% (or, as some manufacturers do, send everything out and hope that some people won't see the difference).

In summary:

If you're going to build a few very specialized systems - you need to use one of the numbered (1-3) approaches above. If you're in mass production - consider averaging the results.

answered Jul 29 '13 at 15:34

Vasiliy

7,323
2
21
38

1

In most assembly lines, a 10% fallout is unacceptable. In the majority of lines, a 1% fallout is unacceptable. If the choice is to use multiple resistors and have a 10% fallout, vs. buying 0.1% or 0.05% resistors then the better tolerance resistors will almost always cost less than having to rework 10% of your product. – Jul 29 '13 at 17:37
@DavidKessner, the discussion about yields and what approach is more profitable is not for this forum. I gave a theoretical example, not an advice. BTW, there are cases when 90% yield is considered superb. The technique of averaging process variations in sensitive applications is used and it is effective. You didn't like the numbers in the example I gave? I can change 10% to 1% if you like it. However the point of my answer won't change. – Vasiliy Jul 29 '13 at 18:06
@DavidKessner, BTW I assumed that in "very sensitive system" described in the question, the option of buying a lower tolerance components will be the first one considered. – Vasiliy Jul 29 '13 at 18:10
1

Every statistic in the linked article assumes that all the resistors are independent, and that's very likely not the case. There will be natural drifts in the production line, and you're likely to buy a bag of resistors that were made near the same time. In the short term, there's no real reason why the mean value will center on the nominal value – Scott Seidman Jul 29 '13 at 18:43
@Scott Seidman, he did not only made math, but took a bunch of resistors and measured them. You can find the results there too. There is also a note about values biasing at the end. Really, you should give this article a bit of attention before commenting. – Vasiliy Jul 29 '13 at 19:02
I actually did, pretty thoroughly, and didn't particularly care for his bootstrapping to defend the statistical argument for an array of parallel resistors, especially given the bimodal distribution. There is no reason why one should assume that the mean of a handful of resistors in a bag should approach the nominal labelled value, as opposed to whatever value within tolerance happens to be rolling of the line for that lot. – Scott Seidman Jul 29 '13 at 19:54
Not nominal labeled value, but the actual mean. This guy explicitly mentioned that the mean of resistors he measured was below the nominal. He also mentioned that this biasing may be performed intentionally by the manufacturer for temperature/aging compensation. – Vasiliy Jul 29 '13 at 20:06

score 0 · Answer 7 · answered Jan 07 '21 at 18:16

0

If you select a carbon resistor of too low resistance, you can tune it up by cutting it slightly with a file and then seal it with nail polish!

answered Jan 07 '21 at 18:16

David G. Pickett

101

This seems to be the essence of Passerby's answer from over seven years ago, but Passerby provided more detail. Did you have something to add? – Elliot Alderson Jan 07 '21 at 21:29

score 0 · Answer 8 · answered Jul 29 '13 at 14:41

One shot answer : You can change the TOLERANCE of the resistor since it is the property of the material which is used to make a resistor. So the better option is go for resistor which has better tolerance instead of thinking to improvise the tolerance manually.

score -1 · Answer 9 · answered Jul 29 '13 at 17:13

-1

Don't forget that the resistor manufacturer is measuring the part's resistance, and culling out those that are close to the desired value to be labeled and sold as higher-precision parts. So if you're looking for 1k ohm parts, 10%, in a bag of parts, I would be surprised to find many samples in the bag that were well within 5%. Ditto 1% - the manufacturer will just sell them as 1% parts...

answered Jul 29 '13 at 17:13

Brooks

98
7

You're speculating, or do you have proof that this is the case? – Jul 29 '13 at 17:30
For some kinds of components, a part which was manufactured in the hopes of it being a 5% part but was off by 7% might be sold as a 10% part, but I doubt that happens much with resistors. Unless things have changed, 5% resistors are usually made from carbon composition while 1% resistors are usually metal film. Since a 1% resistor which measures too high or too low could be sold as the next higher or lower value, there's no real need to sell such parts as 5% resistors. Even if there was a surplus of odd-value parts, it would be simpler to sell them at a discount to distributors... – supercat Jul 29 '13 at 17:49
...who could then have a SKU for "1K 5%" which would translated into "whatever resistor between 960 and 1050 ohms the distributor happens to have the most of", than it would be to have the manufacturers mark them as 1K 5%. – supercat Jul 29 '13 at 17:50
@david-kessner From Ohmite, regarding their carbon-composition resistors: "Carbon composition resistors are manufactured by extruding a blend of carbon and organic binders inside a phenolic outer body. The extrusion is cut to length, leads inserted, cured, and marked to form a finished resistor. The carbon and binder mixture is adjusted to produce different resistance values. The resistors are sorted for 5%, 10%, and 20% tolerance values." – Joe Hass Jul 30 '13 at 16:39
@JoeHass Binning of parts is no surprise to anyone. I was referring to the part about finding parts within 5% resistors in a 10% lot, etc. Indeed, comments from Peter Bennett and Supercat would indicate that this is unlikely or unnecessary. – Jul 30 '13 at 16:55

score -3 · Answer 10 · 2013-07-30T13:18:06.157

-3

You're in luck, there is a method

Let us say you need 10k of resistance. Let us furthermore say you have a limitless supply of 10k resistors - and they're all 10% but you need 5%.

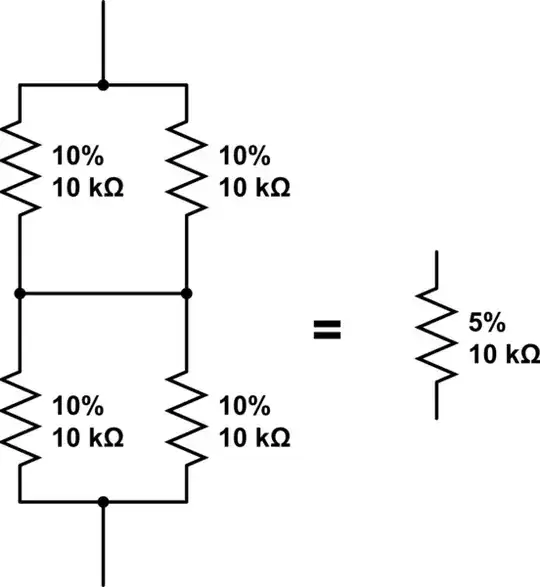
schematic

^{simulate this circuit – Schematic created using CircuitLab}

Be advised: The percentage numbers are NOT exact. I could calculate the actual values if I had my notes nearby.

The brief explanation is: The more components you use, the less uncertainty you have because the errors will tend to average out.

NOTE TO PEOPLE TALKING ABOUT WORST-CASE

Point of order to y'all: Worst-case on a 5% is not 5%, 5% is the 3Sigma worst case. The actual worst case is -100%/+(Unknown)%. If your system absolutely cannot have more than 5% variance, a 5% resistor isn't good enough to GUARANTEE that, either. If you call a resistor 5%, what that MEANS is that out of a production line, you have to go past 3 Standard Deviations to go past 5%

edited Jul 30 '13 at 13:18

answered Jul 29 '13 at 14:29

8

While I agree that the errors would tend to average out, the tolerance is still 10%. Consider the value if all four resistors were 10% high. – Tut Jul 29 '13 at 14:35
Not only that, I don't think there are many situations where this would be cost-effective. – us2012 Jul 29 '13 at 14:36
However, from what i understand, the worst case error would still be 10%. So in a sensitive system this is not an option. If you need 5%, you have to use 5% components. – Rev Jul 29 '13 at 14:38
Exactly ! I agree with Tut here. If you consider the worst case, that is all resistors with (10k + 10% of 10k) then all resistors will take a value 11k. So in effect the resistance is again 11k which shows that there is no change in the tolerance of the resistor. – IamDp Jul 29 '13 at 14:38
@VasiliyZukanov And still, while unlikely, you could have four successive 1K resistors from a tape of 10% parts that all measure 1.1K Ohm. Yeah, the manufacturer could have sold them as 1.1K 1% parts, but where's the guarantee? The point is that medivh's answer is potentially more expensive than a low tolerance part, takes a lot of extra PCB space and still does not save you from measuring the parts with a multimeter to be sure you get into your desired resistance range. – us2012 Jul 29 '13 at 14:45
This answer is just plain wrong. No matter how many high-error resistors you average, the worst case error for the combined resistance will still be the same. – Olin Lathrop Jul 29 '13 at 14:50
@Vasiliy Nobody is denying that. Long-term statistics are useless for a sample of 4 parts in something that OP calls a "highly sensitive system", though. – us2012 Jul 29 '13 at 14:52
What matters here is that 4 resistors manufactured at the same time and on the same reel are likely to have similar properties so its that if one is high or low that they are all high or low. – Warren Hill Jul 29 '13 at 14:57
I've read some materials on the Web and now I see that I'm wrong. Removed all my comments. Sorry guys. – Vasiliy Jul 29 '13 at 15:04
As for reference, I've been reading this: `http://paulorenato.com/joomla/index.php?option=com_content&view=article&id=109&Itemid=4`. This led to this discussion, however, later on, I found that there is no agreement on this subject, therefore this discussion is pointless and I'm wrong. – Vasiliy Jul 29 '13 at 15:08
@medivh "5% is the 3Sigma worst case" I doubt very much that this is true. Do you have a reference. Here's a statement from Ohmite "Carbon composition resistors are manufactured by extruding a blend of carbon and organic binders inside a phenolic outer body. The extrusion is cut to length, leads inserted, cured, and marked to form a finished resistor. The carbon and binder mixture is adjusted to produce different resistance values. The resistors are sorted for 5%, 10%, and 20% tolerance values." This seems to support Brooks. – Joe Hass Jul 30 '13 at 16:36
A lot of people died assuming normal distribution. – shimofuri Jul 30 '13 at 21:02

Reducing the tolerance of resistors manually

10 Answers10

Linked