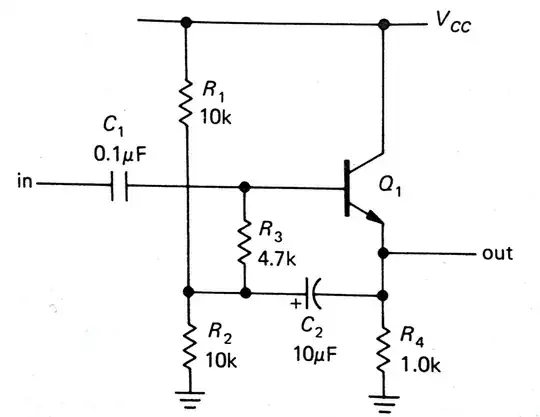
Here's how I would work out the input impedance.
At the frequencies of interest, consider C2 to be a wire.
Note then, that the output voltage appears at the bottom of R3 whilst the input voltage appears at the top.
Let the voltage gain of this circuit be \$A_{CC} < 1\$.
Then the voltage across R3 is \$v_{in} - A_{CC}\ v_{in} = v_{in}(1 - A_{CC})\$
The current through R3 is then \$\dfrac{v_{in}(1 - A_{CC})}{R_3} \$
Thus, to the input voltage source, R3 "looks" bigger by factor of \$\dfrac{1}{1 - A_{CC}} \$
Looking into the base of Q1, the impedance is approximately \$(1 + \beta)\ (R_4||R_2||R_1 + r_e) \$ where \$r_e = \frac{V_T}{I_E} \$.
Then, the input impedance is:
\$r_{in} = \dfrac{R_3}{1 - A_{CC}} || \left[(1 + \beta)\ (R_4||R_2||R_1 + r_e) \right] \$
Since the left hand term in the parallel combination is typically far larger than the right hand term, the input impedance is dominated by the right hand term, i.e.,
\$r_{in} \approx (1 + \beta)\ (R_4||R_2||R_1 + r_e)\$
For example, with \$V_T = 25mV\$ and \$I_E = 1mA\$, \$r_e = 25 \Omega \$ thus, with \$R_4||R_2||R_1 = 833 \Omega \$:
\$r_{in} \approx (1 + \beta)\ 858 \Omega \$