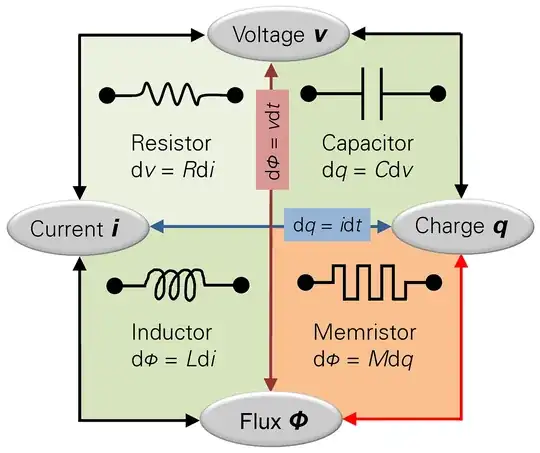
If a resistor is a device where \$\mathrm{d}v = R\mathrm{d}i\$, than resistance is EMF (\$v\$) divided by current (\$i\$), or in SI units, volts \$(V)\$ divided by amperes (\$A\$). We can define the volt in terms of SI base units:
$$ V = \frac{kg \cdot m^2}{A \cdot s^3} $$
The ampere is already an SI base unit. The volt divided by the ampere is then the ohm:
$$ \Omega = \frac{V}{A} = \frac{\frac{kg \cdot m^2}{A \cdot s^3}}{A} = \frac{kg \cdot m^2}{A^2 \cdot s^3}$$
A memristor is where \$\mathrm{d}\phi = M\mathrm{d}q\$, so memristance must be magnetic flux (\$\phi\$) divided by charge (\$q\$), or in SI units, webers (\$Wb\$) divided by coulombs (\$C\$). Defined by SI base units:
$$ Wb = V \cdot s = \frac{kg \cdot m^2}{A \cdot s^2} $$
$$ C = A \cdot s $$
Then the weber divided by the coulomb is our unit of memristance:
$$ \text{unit of memristance} = \frac{Wb}{C} = \frac{\frac{kg \cdot m^2}{A \cdot s^2}}{A \cdot s} = \frac{kg \cdot m^2}{A^2 \cdot s^3}$$
Which, one can see, is identical to the ohm. So, memristance is measured in ohms, just like resistance.
If you don't strip everything to base units, then the equivalence can be more simply expressed:
$$ \require{cancel}
\frac{Wb}{C} = \frac{V \cdot s}{A \cdot s} = \frac{V}{A} = \Omega$$
I find this the most interesting approach, because it can be seen that a memristor integrates both EMF and current (as indicated by the \$\cdot s\$ in the numerator and the denominator). It's as if it's somehow an inductor and a capacitor at the same time, and in doing so, the time terms cancel, and it becomes neither. If you were to remove just one of the \$s\$ terms, then you'd be left with the henry or the farad, but with both you get back to the ohm.
Of course, if \$M\$ in \$\mathrm{d}\phi = M\mathrm{d}q\$ is just a constant, then the time terms really do cancel and you are left with just an ordinary resistor. As Wikipedia puts it:
There is no such thing as a standard memristor. Instead, each device implements a particular function, wherein the integral of voltage determines the integral of current, and vice versa. A linear time-invariant memristor, with a constant value for \$M\$, is simply a conventional resistor.
What makes memristors fancy is that \$M\$ is a function (usually defined as a function of the time integral of current: charge, but could be defined as a function of the time integral of voltage: flux). Because \$M\$ is a function, it allows one to have a device where \$\mathrm{d}v/\mathrm{d}i\$ (usually we'd call that resistance) changes based on what's happened so far: how much current, or how much voltage, there has been in the past. The discrepancy is explained by physical effects I don't really understand, like the arrangement of oxides on microscopic structures, or something. They get rearranged as charge moves through, changing the voltage it will take to move additional charge (resistance).
Inductors and capacitors do this also, but unlike a capacitor, where getting the voltage to \$0V\$ requires bringing the time integral of current, charge, to \$0C\$, and unlike inductors, where getting the current to \$0A\$ requires bring the time integral of voltage, flux, to \$0Wb\$, a memristor can go to \$0A\$ and \$0V\$ without requiring charge or flux to go to zero. Thus, they don't lose their memory of the past when no current or voltage is applied.
That also means if you graph for a memristor voltage on one axis, and current on the other, you don't get a straight line (that would be a resistor), but you do get a hysteresis loop that always passes through the origin, \$0V\$ and \$0A\$. Just where that loop goes at other points depends on the kind of memristor.