Decrease in stored energy after connection of another capacitor

Question

A 3-µF capacitor charged to 100V is connected across an uncharged 6-µF capacitor. So the initial stored energy is: 15mJ and the final: 5mJ. What happen to the 10-mJ of energy?

Answer 1

This problem is a classic and it provides a wonderful example of the limitations of ideal circuit theory.

There are three assumptions underlying ideal circuit theory and one of those assumptions is, essentially, to ignore the self-inductance of the circuit.

But any circuit (closed path) has inductance. So, even if we keep the idealization of zero resistance wire and ideal capacitors, we cannot escape the fundamental inductance of the circuit (unless we shrink the circuit to zero size).

A careful analysis will show that, even if the resistance is zero (or effectively so) so that there is no effective resistive loss, there is energy "lost" to the electromagnetic field; the "lost" energy is radiated away as electromagnetic radiation.

A detailed derivation can be found in A Capacitor Paradox.

Answer 2

It is dissipated in the non-zero resistance of the connecting wires. You can calculate that the dissipation does not depend on the actual resistance, so reducing it does not help.

related: energy in capacitors (there must be more but I can't find them)

Answer 3

As Wounter van Ooijen has already said, it is a matter of parasitic resistance, which is always present. The proof:

EDIT: Even though the answers provided must satisfy any engineer on this planet (joke), it looks like the case of zero resistance wires is still being considered as a scenario of possible violation of conservation of energy (joke).

In fact, a complete answer to this question must address the case of zero resistivity because everyone heard of superconductors. Well, turns out that the same questions have already been asked at Physics forum. One of the best answers may be found here.

Answer 4

Intuition would tell us that if we could somehow connect the capacitors with a zero resistance, than the energy would be conserved. But this is wrong. Our intuition comes from the fact that usually power decreases as resistance approaches zero. For example:

^{simulate this circuit – Schematic created using CircuitLab}

$$P = 1A\cdot V\\ V = 1A\cdot R$$

Therefore, as \$R\to 0\Omega\$, then \$V\to0V\$. Clearly, \$1A\cdot 0V = 0W\$, so we can say:

$$\lim_{R \to 0} (1A)^2R = 0W$$

This is the usual case because although the circuits we make aren't just current sources, they have some resistance somewhere that limits the current. Thus, we are in the habit of thinking minimize unintentional resistance to minimize loss.

Another example:

^{simulate this circuit}

$$ P = 1V \cdot I\\ I = 1V/R $$

Therefore, as \$R\to 0\Omega\$, then \$I\$ gets bigger, and then you hit a division by zero. Therefore, we can't evaluate the limit:

$$\lim_{R \to 0} \frac{(1V)^2}{R}$$

Now, consider that in the instant that you connect the capacitors, they look like voltage sources, and you can see that it's not possible to connect even ideal capacitors with ideal conductors. Even if you connect them with very small resistances, current goes up, \$I^2R\$ losses go through the roof, and you are no better off than had you connected them with a large resistance. There must necessarily be some sort of impedance between the capacitors for this circuit to be mathematically consistent: if it's not a resistance, then perhaps an inductance.

Answer 5

This answer is more or less a further exploration of the energy transfer. Shorting one capacitor to another is of course nonsense if you want to conserve energy. This has been proven in the answers already so I won't dwell on it other than to say "you wouldn't expect a buck voltage converter to work without an inductor". Well, in all seriousness you wouldn't so why could anyone (including me) be dumb enough LOL.

The energy from C1 can be transferred to C2 with zero resistance and this of course relies on the inductance of the wires. If a non-lossy inductor connected C1 to C2, the energy would be conserved and remain oscillating forever between the two capacitors and the inductor. But I thought wouldn't it be cool if it could reach a steady-state. So, I thought what if there were cable resistance - the oscillations would die out BUT the 10mJ energy is still lost in resistor heat dissipation. Then I thought about this: -

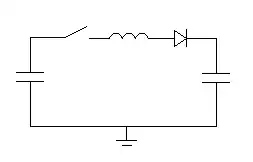
It turns out that with a perfect diode and no losses you can successfully take all the energy from the left cap and put it in the right cap. 15mJ is successfully transferred from a 3uF cap to another 3uF cap and the voltages stabilize out. The diode losses will lose about 2mJ if these are taken into account.

More to follow.

Answer 6

probably I'm not skillful enough to say something interesting (I'm not an electronic engineer, only an electronic enthusiast) but I had to overcome the energy transfer problem through capacitors in the past and I've "partially" found a solution (tested inside my little lab).

The idea is similar to the one schematized by Andy Aka but, instead of a simple inductor, I used a complementary one and, instead of a simple diode, I used a Schottky one (to exploit the avalanche effect): I discovered that with these two components put in series I was able to transfer the 65-70% of the energy from the charged capacitor to the empty one.

I think that the amount/percentage of the transferred energy could depend on the resonance frequency: I had no time nor resources to test all the possible harmonics of that resonance, so further investigation is needed.

If anyone found appreciable solutions about this problem, please come in contact with me: fabrizioricciarelli@gmail.com

Cheers

Devesh