In short, capacitors are two conductive objects, often small plates, separated by something that insulates, known as a dielectric. Much like the static buildup that occurs if you rub a balloon on your arm and put it to your hair, opposite charges build up on either plate, allowing it to store energy in the form of charge.
There are 2 other key factors that influence capacitor behaviour and make them so useful.
-They charge exponentially, not linearly. Say I charge a capacitor with a constant voltage, and I measure the voltage across the capacitor (which corresponds to the charge held within it) every say, 5 seconds. It would not go up in say, 0.1 every 5 seconds. Instead it increases by a set percentage of the total capacity per unit time. This is effectively the same principle (except in reverse) to radioactive decay - the "half-life" is an intuitive concept, corresponding to the time taken for the amount to reduce to 50% of what it was - but not for it to lose a set amount (i.e. it's not 50 molecules per second, it's 50% per second).
It looks something like this:
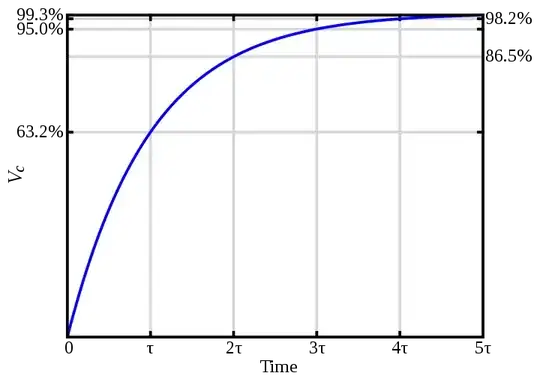
As you can see it charges fast at the start, but then slows down as charge accumulates.
-The second is the consequences of this charge accumulation. As the voltage increases, the current "through" the capacitor drops - apparently increasing the electrical resistance of the capacitor. However, if we were to reverse the polarity of the input power supply, switching them around, it has the effect of "decreasing" the resistance - the charge, rather than being squeezed into the capacitor, can easily flow out and in fact effectively boosts the effective voltage.
The main consequence of this is that the capacitor resists DC, but allows AC. More concretely, the higher the frequency of the voltage polarity switching (i.e. AC), the less the capacitor will impede the flow of current in circuit.
The capacitor can be thought of as an electric spring. You push down on it, symbolising current flowing into it. At first it offers little resistance. However, as you keep pushing, the spring pushes back harder, until you can effectively push no more. This is equivalent to the voltage across the capacitor (again equivalent to charge stored within it) getting close to the input voltage - like the upward force of the spring balancing out against your weight.
Now what happens if you push in the opposite direction? The spring works with you instead of against you, increasing the output force past what you could hope to achieve with your muscles and weight alone.
So how can we exploit this? There are two main types of capacitor usage depending on how they are arranged in a circuit - "coupling", where the capacitor is in series, and "decoupling", capacitor in parallel. Both make use of these aforementioned principles.
Coupling are used in blocking DC - this is most often found in signal processing and radios. The smaller the capacitor, the higher the frequency it impedes (as it charges faster), so by adjusting capacitance, we can adjust frequencies blocked. When used with an inductor (the diametric opposite of a capacitor) - the most relevant property of which is the blocking of HIGH frequencies, we can restrict signals into a particular "band" of frequencies - a "band pass" circuit. This is critical in radios to transmit or receive at the desired frequency.
Coupling capacitors are also used in timing circuits - since transistors (electronic switches) turn on at a known voltage, and capacitors charge at a known rate, they can be used to only turn the transistor on at a certain time (or frequency).
Decoupling capacitors are used either for energy storage or for electrical "damping". Again, it helps to think about it in terms of a spring.
A spring in a pellet gun shows the energy storage perfectly. The spring is pulled back, analogous to the capacitor being charged, then released, allowing it to discharge its energy into a "load" - mechanically speaking, the pellet (or other ammunition), electrically, a component, say, a light. Capacitors are ideal for situations in which lots of energy is needed in a short period of time, since they discharge extremely quickly - for instance, a defibrillator. The battery alone could not possibly discharge all the required energy so quickly, so the internal capacitor instead stores it and releases as required.
For the damping, it's best to think of the capacitor/spring analogy as the spring in car suspension. Car suspension protects the car (and passengers) from damage by absorbing some of the energy of the vertical movement of the car. If a wheel is pushed up very quickly by going over a large stone, the rest of the car is less affected thanks to the suspension, which absorbs energy then releases it slowly by pushing the car up. In the same way, a decoupling capacitor can "smooth out" electrical signals or pulses. Analogous to the stone, sometimes the nature of electrical generation, or malfunctions, can cause voltage "spikes". Even very short voltage spikes can cause severe damage to some equipment. The decoupling capacitor is able to absorb this "shock" and reduce the chance of damage occuring. In addition, it can be used to produce smoother transitions between states - like a light fading out, even after the switch has been turned off.
Hope that helps. Sorry if it's a bit verbose, but I aim to be comprehensive.
