Here is an answer which is more rough, but easy to recall and useful as a first approximation.
Only the case of a NPN bipolar junction transistor is dealt here; things are similar for PNP bipolar junction transistors.
The basic assumption is that the B-E current is negligible with respect to the current through the collector, so, the collector current is approximately equal to the base current: $$I_E = I_C = I.$$
If this assumption does not hold, then the transistor is probably misused or subject to a catastrophic failure.
Now, the power dissipated by the transistor is of course $$P = V_{CE} I.$$
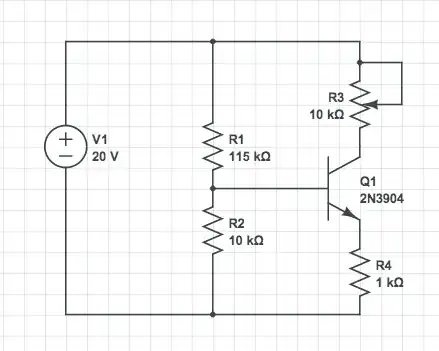
To obtain an upper bound that is useful in the general case, we model the problem by considering that the collector is connected to \$V_{CC}\$ through a resistor \$R_3\$, and that the base is connected to the ground through a resistor \$R_4\$ (this includes the load etc.). This is exactly the case in the OP problem. We have:
$$V_{CE} = V_{CC} - R_3 I - R_4 I = V_{CC} - (R_3+R_4)I,$$
hence
$$P = (V_{CC} - (R_3 + R_4)I) I.$$
Using infinitesimal calculus, you find this expression of P is maximal whenever $$I = V_{CC}/2(R_3+R_4),$$ and equal to
$$P^* = V_{CC}^2/4(R_3+R_4).$$
This is the desired upper bound for the dissipated power whenever \$R_3\$ and \$R_4\$ are known. It means that:
Theorem: the power dissipated by the transistor is not larger than \${1\over 4}\$ of the power that would be dissipated by the two resistors \$R_3\$ and \$R_4\$ if they were directly connected.
In the OP problem, \$R_3\$ is furthermore allowed to vary between 0 and 10kOhm, so, it is obvious that the expression of \$P^*\$ will be maximal for \$R_3=0\$. This gives the upper bound $$P^{**} = V_{CC}^2/4R_4 = 100mW,$$ larger than, but not so far from, Olin Lathrop's bound.