Comparator with hysteresis equation for Vmax Vmin

Question

In a scientific paper I came across the comparator circuit with hysteresis shown in the picture. The authors of the paper use this circuit to control the voltage at a capacitor. If the voltage at the capacitor exceeds a level Vdc,max the comparator should output high, if the voltage falls below the level Vdc,min the comparator should output low. The reference voltage of the comparator is set with Zener diode D3. R3 is used to limit the current through the Zener diode. I would now like to derive the equations for Vdc,min and Vdc,max given in the paper myself but fail at times.

As a first approach I tried to solve it using the voltage divider approach as soon as the voltage at the positive input is greater than Vz the comparator should switch, before that the output must be at Vcc-Low = GND. Therefore the voltage at R2 has to be determined. is this the right approach?

Answer 1

If the voltage at the capacitor exceeds a level Vdc,max the comparator should output high, if the voltage falls below the level Vdc,min the comparator should output low.

The comparator with hysteresis may not be a solution to your problem. Because with hysteresis, the max and min points change slightly around the original reference point (the reference without the hysteresis).

So window comparator might be what you need:

---

If the comparator with hysteresis what you need, here's your answer:

is this the right approach?

I couldn't understand your approach but here's how I calculate:

Without the extra resistor (from output to non-inverting input) the trigger point would be the reference voltage (voltage at the inverting input). Quite simple:

^{simulate this circuit – Schematic created using CircuitLab}

With the extra resistor the division ratios will change. Assume the comparator gave an output of HI (VCC):

^{simulate this circuit}

So if you calculate Vtrig_HI from the divider network above that'll be the max trigger point.

Likewise, assume the comparator gave an output of LO (GND):

^{simulate this circuit}

Again, if you calculate Vtrig_LO from the divider network above that'll give you the min trigger point.

---

EXAMPLE:

VX = 10V, R1 = 10k, R2 = 1k, and comparator's supply is VCC = 5V.

Without any hysteresis the trigger point would be 2V.

But if we add an extra resistance of R3 = 20k for hysteresis, using the two diagrams above, the low trigger would be 1.92V and the high trigger would be 2.11V.

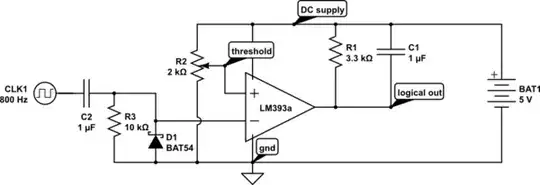
^{simulate this circuit}

For HI, solve the following for Vtrig-HI:

$$ \mathrm{ \frac{10V-V_{trig-HI}}{4k}+\frac{5V-V_{trig-HI}}{20k}=\frac{V_{trig-HI}}{1k} } $$

And for LO, solve the following for Vtrig-LO:

$$ \mathrm{ V_{trig-LO} = 10V \cdot \frac{(1k \ || \ 20k)}{4k+(1k \ || \ 20k)} } $$

---

You can derive the equations if you want. During a design, I normally put the calculations into an Excel file and play with the values (cells) to see how trigger points change.

Answer 2

This is how I would approach the problem. Below is the circuit drawn with nodes Z and X, where Z has fixed reference potential \$V_Z\$, and X has potential \$V_X\$ that is a function of both output \$V_{OUT}\$ and the supply \$V_{DC}\$:

^{simulate this circuit – Schematic created using CircuitLab}

You have two conditions to consider, output high, \$V_{OUT} = V_{DC}\$, and low, \$V_{OUT} = 0V\$. In the former case, we have a network of resistances connected as shown below left, and the latter situation on the right:

^{simulate this circuit}

The algebra is easier if we treat the supply DC and resistors R1 and R2 as their Thevenin equivalent:

^{simulate this circuit}

where:

$$ V_{TH} = V_{DC}\frac{R_2}{R_1+R_2} $$

$$ R_{TH} = R_1 \parallel R_2 = \frac{R_1R_2}{R_1 + R_2} $$

The resistor networks in each situation (high and low output) are therefore equivalent to these:

^{simulate this circuit}

These are simple resistor potential dividers, the only difference between the two being the presence/absence of the voltage source \$V_{DC}\$. The potentials at X are trivial to write:

$$ V_{X(H)} = V_{DC} + (V_{TH} - V_{DC})\frac{R_5}{R_4 + R_5 + R_{TH}} $$

$$ V_{X(L)} = V_{TH}\frac{R_5}{R_4 + R_5 + R_{TH}} $$

You may have noticed that R4 is redundant. It's effectively in series with the other two resistances R5 and Rth. You can obtain exactly the same values for \$V_X\$, in both states, by removing it altogether, and adjusting Rth and/or R5 to compensate. I won't do that here, it's just a heads-up.

Now you can substitute back in the expressions for \$V_{TH}\$ and \$R_{TH}\$ from before. The last step is to equate \$V_{X(H)} = V_Z\$ and \$V_{X(L)} = V_Z\$, which I think you can handle from here. You should end up with expressions for \$V_{X(H)}\$ and \$V_{X(L)}\$ in terms of only the resistances and \$V_{DC}\$.

Answer 3

One way to immediately write down the answer is to do a Wye-Delta transformation on R1, R2, R4.

Then (picking the more complex one, because why not) we can immediately write:

\$ \frac{V_{MIN}}{V_Z} = \frac{R_5 ||R_{AC}}{R_{BC}} +1 \$

where \$R_{AC} = \frac{R_1 R_2 + R_1 R_4 + R_2 R_4}{R_2}\$ and \$R_{BC} = \frac{R_1 R_2 + R_1 R_4 + R_2 R_4}{R_1}\$

A bit of manipulation later and you'll see that the authors of the paper missed an added R1*R2 in both numerator and denominator, which might explain why you are having problems deriving their equation.

I'll leave the other derivation to you.

Answer 4

Looking for the minimalistic solution...

This "scientific solution" caught my attention firstly with its many resistors, secondly with its single power supply, thirdly with the fact that the input signal serves as a power supply, and finally with the strange shape of its output signal which follows the input. I instinctively felt that it could be simplified and felt the desire to do so, albeit with less than "scientific methods". In the end, I was able to reduce the number of resistors by two. Here is how I did it.

5-resistor solution

In the original OP solution, the input voltage is scaled down twice with a voltage divider R2-R4 and applied to the input of a non-inverting comparator with hysteresis. Through the voltage divider R5-R3, a positive feedback is realized through which the hysteresis is obtained.

^{simulate this circuit – Schematic created using CircuitLab}

4-resistor solution

If we make the voltage divider R2-R4 high enough resistive, it can also perform the functions of the input resistor R5; so we can remove the latter.

^{simulate this circuit}

3-resistor solution

And finally, we can try to assign the functions of the R2-R4 voltage divider to the input resistor R5 (R2 in the schematic below).

^{simulate this circuit}

In my opinion, the circuit should not work at its lower threshold because the reference voltage on the Zener diode ceases to be constant... but the graph shows hysteresis. This mystery should be cleared up...

Conclusion

In general, I think that supplying the op-amp from the input signal is not a good idea.