Derive a State-Space Model for an Electric Circuit with three Energy Storage Components

Question

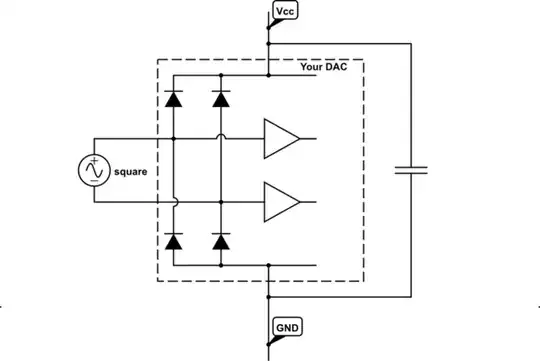
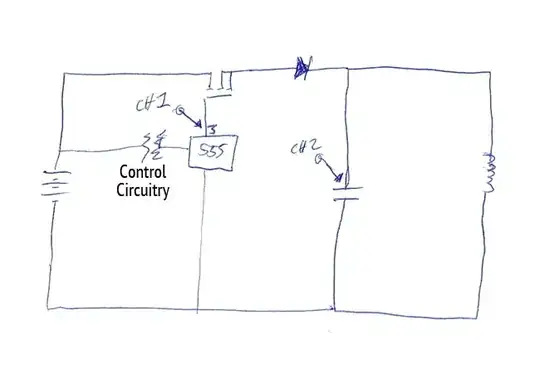
I want to model the shown circuit diagram with a state-space model. However, I cant solve it since I obtain four unknown variables while only three of the derived equations are linear independent. Here is how I obtained my equations:

The choosen loops are according to the picture below.

All 6 possible Kirchhoff voltage equations (clockwise) are

\begin{align} V_{C1}-V_{R1}=0 \qquad (1) \\ V_{R2}+V_{C2}-V_0-V_{R0}-V_{C1}-V_L=0 \qquad (2) \\ V_{DC}-V_{C2}-V_{R2}=0 \qquad (3) \\ V_{R2}+V_{C2}-V_0-V_{R0}-V_{R1}-V_L=0 \qquad (4) \\ V_{DC}-V_0-V_{R0}-V_{C1}-V_L=0 \qquad (5) \\ V_{DC}-V_0-V_{R0}-V_{R1}-V_L=0 \qquad (6) \end{align}

According to graph theory, only three KVL equations are linear independent. Various combinations are possible:

1. Set of independent equations: (1) + (2) + (3)
2. Set of independent equations: (1) + (3) + (4)
3. Set of independent equations: (1) + (3) + (5)
4. Set of independent equations: (1) + (3) + (6)
5. Set of independent equations: (1) + (4) + (6)

The two Kirchhoff’s current equations are

\begin{align} i_{R1}=-i_L-i_{C2}-i_{C1} \qquad (7) \\ i_{R0}=i_{C1}+i_{R1} \qquad (8) \end{align}

Inserting (7) in (8) gives

\begin{equation} i_{R0}=-i_L-i_{C2} \qquad (9) \end{equation}

The choosen states are

\begin{align} x_1 = V_{C1} \qquad (10) \\ x_2 = V_{C2} \qquad (11) \\ x_3 = i_{R0} \qquad (12) \end{align}

The inputs are unnumbered as they are not important for the derivation:

\begin{align} u_1 = V_0 \\ u_2 = i_L \end{align}

The equations for the capacitances are

\begin{align} i_{C1} = C_1\cdot\dot{V_{C1}} = C_1\cdot\dot{x_1} \qquad (13) \\ i_{C2} = C_2\cdot\dot{V_{C2}} = C_2\cdot\dot{x_2} \qquad (14) \end{align}

The equation for the inductance is $$ V_{L} = L\cdot\dot{i_{R0}} = L\cdot\dot{x_3} \qquad (15) \\ $$

Equation (7) together with (13) and (14) becomes $$ i_{R1} = -i_L - C_2 \cdot \dot{x}_2 - C_1 \cdot \dot{x}_1 \qquad (16) $$ Equation (9) together with (14) becomes $$ i_{R0} = -i_L - C_2 \cdot \dot{x}_2 \qquad (17) $$

By using equations (10)-(17), the KVL equations (1)-(6) can be brought into the following form:

\begin{align} x_1 + R_1 \cdot i_L + R_1 \cdot C_2 \cdot \color{red}{\dot{x}_2} + R_1 \cdot C_1 \cdot \color{red}{\dot{x}_1} = 0 \qquad (1') \\ (R_2 \cdot C_2 + R_0 \cdot C_2) \cdot \color{red}{\dot{x}_2} + x_2 - V_0 + R_0 \cdot i_L - x_1 - L \cdot \color{red}{\dot{x}_3} = 0 \qquad (2') \\ \color{red}{V_{\text{DC}}} - x_2 - R_2 \cdot C_2 \cdot \color{red}{\dot{x}_2} = 0 \qquad (3') \\ (R_1 \cdot C_2 + R_2 \cdot C_2 + R_0 \cdot C_2) \cdot \color{red}{\dot{x}_2} + x_2 - V_0 + (R_0 + R_1) \cdot i_L + R_1 \cdot C_1 \cdot \color{red}{\dot{x}_1} - L \cdot \color{red}{\dot{x}_3} = 0 \qquad (4') \\ \color{red}{V_{\text{DC}}} - V_0 + R_0 \cdot i_L + R_0 \cdot C_2 \cdot \color{red}{\dot{x}_2} - x_1 - L \cdot \color{red}{\dot{x}_3} = 0 \qquad (5') \\ \color{red}{V_{\text{DC}}} - V_0 + (R_0 + R_1) \cdot i_L + (R_0 \cdot C_2 + R_1 \cdot C_2) \cdot \color{red}{\dot{x}_2} + R_1 \cdot C_1 \cdot \color{red}{\dot{x}_1} - L \cdot \color{red}{\dot{x}_3} = 0 \qquad (6') \end{align}

The detailed derivation of KVL equations (1')-(6') are further down. They should be correct. My problem is as stated before: I only have three linear independent equations, e.g. (1) + (3) + (5). However, as marked in red, using these 3 equations will result in 4 unknown parameters. Thus, I cannot solve for \$\dot{x_1}\$, \$\dot{x_2}\$ and \$\dot{x_3}\$ without them being a function of \$V_{DC}\$. The voltage \$V_{DC}\$ is the voltage across the ideal current source and results from applying the current \$i_L\$ to the circuit. Any help is greatly appreciated.

Detailed derivation of equations (1')-(6'):

Answer 1

First of all I'll present a method that uses Mathematica. Secondly, I assume that the voltage \$\text{V}_0\$ is defined by a voltage source and \$\text{I}_0\$ is defined by a current source. I'll maybe rename resistors, capacitors, inductors, voltages and currents but it will be clear because of the circuit redawn below.

---

Well, we are trying to analyze the following circuit:

^{simulate this circuit – Schematic created using CircuitLab}

When we use and apply KCL, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\text{I}_2+\text{I}_4\\ \\ \text{I}_5&=\text{I}_2+\text{I}_4\\ \\ \text{I}_5&=\text{I}_0+\text{I}_3\\ \\ \text{I}_1&=\text{I}_0+\text{I}_3 \end{alignat*} \end{cases}\tag1 $$

When we use and apply Ohm's law, we can write the following set of equations:

$$ \begin{cases} \begin{alignat*}{1} \text{I}_1&=\frac{\displaystyle\text{V}_0-\text{V}_1}{\displaystyle\text{R}_1}\\ \\ \text{I}_2&=\frac{\displaystyle\text{V}_1-\text{V}_2}{\displaystyle\text{R}_2}\\ \\ \text{I}_4&=\frac{\displaystyle\text{V}_1-\text{V}_2}{\displaystyle\frac{1}{\text{sC}_1}}\\ \\ \text{I}_5&=\frac{\displaystyle\text{V}_2-\text{V}_3}{\displaystyle\text{sL}}\\ \\ \text{I}_3&=\frac{\displaystyle\text{V}_3-\text{V}_4}{\displaystyle\text{R}_3}\\ \\ \text{I}_3&=\frac{\displaystyle\text{V}_4-0}{\displaystyle\frac{1}{\text{sC}_2}} \end{alignat*} \end{cases}\tag2 $$

The Mathematica code to solve these systems of equations is given by:

Clear["Global`*"];
R1 =;
R2 =;
R3 =;
C1 =;
C2 =;
L =;
V0 = LaplaceTransform[(*place here the (time dependent) input signal \
of the voltage source*), t, s];
I0 = LaplaceTransform[(*place here the (time dependent) input signal \
of the current source*), t, s]; FullSimplify[
 Solve[{I1 == I2 + I4, I5 == I2 + I4, I5 == I0 + I3, I1 == I0 + I3, 
   I1 == (V0 - V1)/R1, I2 == (V1 - V2)/R2, I4 == (V1 - V2)/(1/(s*C1)),
    I5 == (V2 - V3)/(s*L), I3 == (V3 - V4)/R3, 
   I3 == (V4 - 0)/(1/(s*C2))}, {I1, I2, I3, I4, I5, V1, V2, V3, V4}]]

Answer 2

I just found the solution. I was neglecting equation (12). Equating (12) and (17) gives

$$ x_3 = -i_L - C_2 \cdot \dot{x_2} $$ Solving for \$\dot{x_2}\$ gives $$ \dot{x_2} = -\frac{1}{C_2}\cdot i_L - \frac{x_3}{C_2} $$

Thats my missing equation. \$\dot{x_1}\$ is obtained by inserting \$\dot{x_2}\$ in (1'). \$\dot{x_3}\$ is obtained by inserting \$\dot{x_2}\$ in (2').

I got it. Thanks.