Visualizing the propagation of signals in digital electronic circuits

Question

I am currently studying Computer Science, and in my Digital Electronics course, I was taught the basic stuff required for computer design.

Also, I've recently started watching Ben Eater's videos on building a small computer on a breadboard, and I've realised just how much I don't know yet about digital electronics.

However, the theory goes into transistors, resistors and capacitors, i.e. stuff which I don't know much about. So, I wanted to build an intuitive understanding of computer design, starting at logic gates and without going down further into the territory of Physics.

The timer used to generate clock pulses is built using transistors, resistors, etc., and I kind of know how it works, but I couldn't understand exactly how a logic gate works, and I don't intend to either.

So, here's a very simple circuit to demonstrate my visualization of how the signals propagate in a digital electronic circuit.

Let red represent high and blue represent low. Also, let there be a buffer queue at each logic gate, whose size depends upon the propagation delay of that gate.

---

Now, the A input is turned to high, either manually or through a clock signal.

---

---

Can I use this as a visual understanding of how the signals propagate?

Answer 1

The whole "buffer queue" thing is unnecessarily complicated. Don't worry at this stage about the propagation along wires — you can assume for now that the entire wire (node) changes state all at once. Gate delay is just a matter of a time delay before the output changes to match what the inputs say it should be.

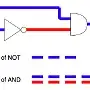
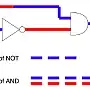
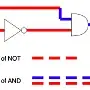
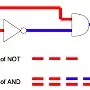
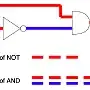
We normally represent this as a timing diagram, something like this:

Node   Time -->
                      ______________________________________
A      ______________/
                     :----->: delay of NOT gate
       _____________________
NOT                  :      \_______________________________
                     :------------>: delay of AND gate
                            :------------>: delay of AND gate
                                   :______:
AND    ____________________________/      \_________________

In a real circuit, the AND gate's output might or might not change in this scenario; it depends on its internal construction.

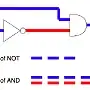
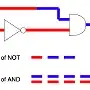
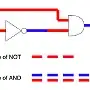
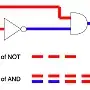
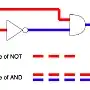
If the NOT gate delay is longer than the AND delay, then you probably will get a pulse:

                      ______________________________________
A      ______________/
                     :----------->: delay of NOT gate
       ___________________________
NOT                  :            \_________________________
                     :------>: delay of AND gate
                             :    :------>: delay of AND gate
                             :____________:
AND    ______________________/            \________________

This is what is called a "race condition", and the output pulse is commonly called a "glitch" and is often an undesirable effect. The existence or width of the pulse depends only on gate delays and is therefore unreliable.

Real gates may have different propagation times for a low-to-high transition at the output versus a high-to-low transition. Furthermore, because of manufacturing variations, each of those delays will have a range of values rather than a single value. For example, for an inverter (NOT gate), you might have:

       ______                       ________________
IN           \_____________________/
  t_PLH(max) :---->:    t_PHL(max) :------->:
  t_PLH(min) :->:  :    t_PHL(min) :--->:   :
                :___________________________:
OUT    _________////                     \\\\_______

where something like \$t_{PLH(max)}\$ means "propagation time, low-to-high, maximum". These are the numbers you'll see in a manufacturer's data sheet for a logic gate. As you add more gates, the uncertainty in the output timing keeps growing. When designing synchronous logic, the maximum delays will be used in the calculation of the setup time to a register, while the minimum delays¹ will be used in calculating the hold time. As you might guess, this can quickly get complicated.

Anyway, I hope this gives you a more conventional way of thinking about timing at the gate level.

---

¹ Minimum delays are sometimes called "contamination delay" these days, but we never used that term when I was learning this stuff.

Answer 2

That is one way to think of it, but as you investigate further into lower levels, you will find ways in which it breaks down. Notice that an ideal buffer or transmission line has infinite bandwidth, that is the delay, and gain (or for digital purposes, the ability to read a 0/1 correctly) don't depend on frequency. Real devices have such limitations.

One way to implement this on your "buffer" strategy, would be to imagine there is some "leakage" between "buckets"; and the number of "buckets" is fixed by design.

As it happens: a real, say, 74HC04 NOT gate, is composed of three gates (each made of two transistors), each of which could be considered a "bucket" (this ultimately comes from node capacitance). The buckets are "lossy" in that, while one is being filled up (at finite speed due to the resistance of the transistor(s) feeding it), it starts "spilling over" to the next (the next transistors begin turning on). This limits how fast the device can actually switch, and therefore doesn't result in indeterminate frequencies being generated when you tie one in a loop for example.

The deeper insight here is, reactive elements -- inductors and capacitors in lumped-equivalent circuits, transmission lines in length-dependent circuits, and free fields in the most general (length, width and height dependent) case -- are the analog representations of state, and how their voltages/currents change, gradually, over time, is in a sense equivalent to the flow of data through registers in a digital system.

That is somewhat getting ahead of your proposed method of study, I suppose, but suffice it to say, there is an explanation and implementation of these concepts in the immediate next level down.

---

On a separate note, be VERY careful using schematic notation to express delays in wires (transmission lines). When we draw a schematic, the default meaning is as a lumped-equivalent circuit, that is, only RLC and active components. Alternately, either the circuit can be considered to be zero size or non-dimensional (pointlike), or the speed of light can be assumed infinite. Neither of which are true in reality, so we must be careful how we express a system in schematic form, whether it be for modeling purposes (in which case we should express such delays as transmission line components), or when the schematic is just a representation of physical wiring.