It's a poor reflection upon the patent system that something so "obvious to those skilled in the art" gets accepted, let alone with such regularity, but alas, here we are.
It also helps to actually be skilled in the art, which, at least at a cursory reading, they weren't?
Mind, I don't particularly care to read the whole thing, so I haven't.
I did find this further down,
In addition, the anode voltage generator 110 and the cathode voltage generator 120 include feedback controllers 150 a and 150 b configured to control the multiple switching circuit 132, respectively. PWM signal which is outputted from each of the feedback controllers 150 a and 150 b may have phase difference of 180/N degrees.
It's not clear if it's simply legalese that they stipulate 180 degrees or "any angle" and allow "180/N degrees" (well, clearly "any" supersedes the rest!), when exactly one of those holds any advantage. Indeed one could further refine the claim to say, phase of each module being within 90/N of its intended angle, so that a range is still captured (i.e. you can't evade the patent claim by making a 91°-phase-interleave machine) while emphasizing the functional claim. Or maybe they couldn't get that, because that was patented decades ago (if it was at all, I don't know). It all seems so obvious that I doubt there was any consideration of "is it patentable".
Anyway.
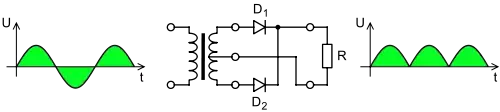
If you cut out the inverter and resonant network and assume any abstract mostly-sinusoidal source, they're basically saying this.

simulate this circuit – Schematic created using CircuitLab
This is an acceptable simplification because, for identical inverters, resonant networks, transformers, rectifiers and filters (just replicate everything in the stack), the phase between them will be equal, regardless of waveform; and being resonant, we can assume a waveform somewhere between sine-ish and square-ish (it's not going to be some weird multi-loop squigglefest).
In this model, the sources are identical, with one flipped upside down i.e. 180 degree phase shifted. The consequence of this should already be obvious: both full-wave voltage doubler rectifiers already perform the frequency-doubling function (notice the output ripple is 2kHz, while the input is 1kHz, hence "full wave"), and if we rotate the phase of the fundamental by 180°, the 2nd harmonic gets shifted by 360°, which is to say, nothing at all.
They clearly show full-wave voltage doublers at the output, so this is apparently their claim. An anti-claim, nothing at all. Huh.
If we were to assign another phase angle instead, we might find these peaks starting to cancel out. In fact we find a minima in output ripple at 90° (because the 2nd harmonic is shifted 180° -- bingo!). And so on, as we stack more modules we can use finer phase increments to cancel out each desired harmonic.

simulate this circuit
Here, one source is set to 90° phase. Note the cancellation: